exercice produit scalaire

[noamii]

dans la figure si contre ABCD est un rectangle tel que AB=2 et AD=3
E est le point de [BC[ et F est le point de [CB[ tel que CE=BF=1

1. calculer BC.BD ,BC.DA, FD.FE (tous des vecteurs)
   2)a/calculer DE.DC et ED.CF
   b/montrer alors que DE.DF=0 et que (DE) est perpendiculaire à (DF)}
   3/soit C={M appartenant à P tel que: MB²+3MC²=16}
   a/vérifier que CB+3CE=0
   b/vérifier que MB²+3ME²=4MC²+12
   c/ en déduire l'ensemble C
   .

pouvez vous m'expliquer comment faire dans la 3eme question de l'exercice 1:
démontrer que: MB²+3ME²=4MC²+12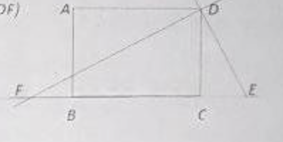

Schéma mis en ligne par la modération du site.

[noamii]

@noamii ce sont tous des vecteurs juste je ne trouve pas le symbole

[Noemi]

@noamii Bonjour,

Pour la question indiquée, utilise la relation de Chasles.
${\overrightarrow{MB}}^2+3{\overrightarrow{ME}}^2=(\overrightarrow{MC}+\overrightarrow{CB}{)}^2+3(\overrightarrow{MC}+\overrightarrow{CE}{)}^2=....$