vecteurs , droites et plan dans l'espace

bonjour,
ABCDEFGH est un cube et O est le centre de la face ABCD. On définit le point M à l'aide de l'égalité vectorielle suivante :
vecteur OM = 1/3 du vecteur OA +1/3 du vecteur AE
je n'arrive a écrire le vecteur CM avec les vecteurs CB, CD et CG .

@Agnès-quintil Bonsoir,

Utilise la relation de Chasles :
$CM→=CO→+OM→\overrightarrow{CM}=\overrightarrow{CO}+\overrightarrow{OM}$
$CM→=CO→+13OA→+13AE→\overrightarrow{CM}=\overrightarrow{CO}+\dfrac{1}{3}\overrightarrow{OA}+\dfrac{1}{3}\overrightarrow{AE}$
Et
$CO→=OA→=12CA→=12(CB→+CD→)\overrightarrow{CO}=\overrightarrow{OA}=\dfrac{1}{2}\overrightarrow{CA}=\dfrac{1}{2}(\overrightarrow{CB}+\overrightarrow{CD})$
Et
$AE→=CG→\overrightarrow{AE}=\overrightarrow{CG}$

Je te laisse terminer et conclure.

Bonjour,

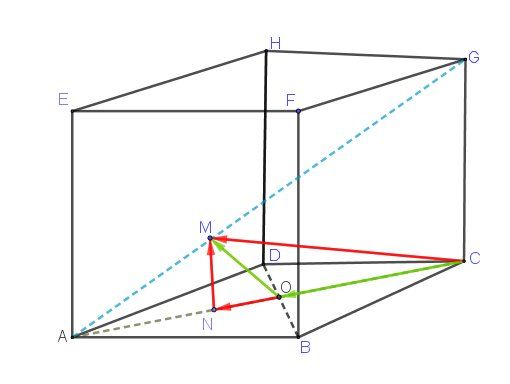
Un schéma (approximatif) pour éclairer l'exercice

$ON→=13OA→\overrightarrow{ON}=\dfrac{1}{3}\overrightarrow{OA}$
$NM→=13AE→\overrightarrow{NM}=\dfrac{1}{3}\overrightarrow{AE}$

bonjour,
je n'arrive pas à donner les coordonnée de A, M et G mais aussi à montrer que les points A,M et G sont aligné

Bonjour,
@Agnès-quintil , ce serait bien de commencer par remercier @Noemi pour l'aide qu'elle t'a apportée.

Tu as dû trouver :
$CM→=23CB→+23CD→+13CG→\overrightarrow{CM}=\dfrac{2}{3}\overrightarrow{CB}+\dfrac{2}{3}\overrightarrow{CD}+\dfrac{1}{3}\overrightarrow{CG}$

@Agnès-quintil a dit dans vecteurs , droites et plan dans l'espace :

bonjour,
je n'arrive pas à donner les coordonnée de A, M et G mais aussi à montrer que les points A,M et G sont alignés

Comme tu ne dis pas dans quel repère tu travailles, ce n'est pas possible de donner des coordonnées de points...
Il faut compléter ton énoncé.

@Agnès-quintil

As-tu terminé les calculs ?
$CM→=23CB→+23CD→+13CG→\overrightarrow{CM}=\dfrac{2}{3}\overrightarrow{CB}+\dfrac{2}{3}\overrightarrow{CD}+\dfrac{1}{3}\overrightarrow{CG}$

Propose tes éléments de réponse pour les coordonnées.
Le repère est-il ? : $(C;CB→;CD→;CG→)(C;\overrightarrow{CB} ; \overrightarrow{CD}; \overrightarrow{CG})$

Dans ce cas $A (1; 1; 0)$

Vu la question relative à $CM→\overrightarrow{CM}$ , j'imagine (? ? ? ) que le repère considéré est $\overrightarrow{CB}, \overrightarrow{CD}, \overrightarrow{CG})$
Si c'est ça, les coordonnées de $M$ sont "évidents " $(23,23,13)(\dfrac{2}{3}, \dfrac{2}{3}, \dfrac{1}{3})$

Pour $A$ , on obtient $(1, 1, 0)$ et pour $G (0, 0, 1)$

En calculant les coordonnées des vecteurs, on arrive à :
$AM→=13AG→\overrightarrow{AM}=\dfrac{1}{3}\overrightarrow{AG}$
d'où la réponse.

@Noemi , bonjour,
Je t'avais vu déconnectée...d'où ma réponse.

@Noemi merci j'ai bien trouvé cette réponse

@mtschoon merci de votre aide

oui c'est un autre exercice désolé j'y penserai la prochaine

OK @Agnès-quintil .

@Noemi a fait le job de déplacement du second exercice
https://forum.mathforu.com/topic/33254/vecteurs-et-faisceaux-lumineux/11

Merci à elle.