Vecteurs et faisceaux lumineux
-
AAgnès quintil dernière édition par Noemi
bonjour,
dans le repère (O; vecteur i ; vecteur j ; vecteur k ) ci-dessous , on représente un plan P passant par le point A(-5;0;0) et de base (vecteur j; vecteur k) . Ce plan représente la façade d'un immeuble que l'on souhaite éclairer grâce à des faisceaux lumineux assimilés à des droites .
1a) justifier que le faisceau lumineux passant par le point de coordonnée (1;1;0) et de vecteur directeur i éclaire la façade?
1b) quelles sont les coordonnées du point d'impact de ce faisceau sur la façade ?
2) justifier que le faisceau lumineux passant par les points de coordonnées (1;2;3) et (1;3;5) n'éclaire pas la façade , c'est à dire qu'il n'a pas de point d'impact avec celle-ci .
3) un faisceau lumineux passe par le point de coordonnées (-1;-2;1) et atteint la façade de l'immeuble au point de coordonnées (-5;1;6).
ce faisceau passe par le point de coordonnées (7;y;z), avec y et z réels . Déterminer les valeurs de y et z
je n'arrive pas a cette exercice pouvez vous m'aider s'il vous plaît merciPost déplacé par la modération du site.
-
mtschoon dernière édition par

@Agnès-quintil , re-bonjour.
C'est très bien si tu es arrivée à terminer l'exercice précédent.Par contre , cet énoncé semble être un nouvel exercice.
Dans ce cas , il faut ouvrir une autre discussion, car ici :
un exercice=une discussion.
-
@Agnès-quintil Bonjour,
J'ai déplacé l'énoncé avec un nouveau sujet car comme indiqué par mtschoon, un seul exercice est à proposer par post.
Indique tes éléments de réponse et la question qui te pose problème.
-
AAgnès quintil dernière édition par
tous car je n'arrive pas à comprendre l'énoncé et les questions
-
Il manque la figure.
-
AAgnès quintil dernière édition par
 url de l'image)
url de l'image)
-
Que peut-on dire du vecteur i→\overrightarrow{i}i par rapport au plan PPP ?
-
AAgnès quintil dernière édition par
j'aurai dit que c'était un vecteur normal
-
Oui, le vecteur i→\overrightarrow{i}i est normal au plan PPP donc ....
-
AAgnès quintil dernière édition par
je sais juste que les coordonnée d'un vecteur normal (a,b)
-
Complète ta phrase,
Que veut dire normal ?
-
AAgnès quintil dernière édition par
il est parallèle au plan
-
Non, perpendiculaire au plan.
Et une flèche qui arriverait perpendiculaire au plan toucherait-elle le plan ?
-
AAgnès quintil dernière édition par
oui elle toucherai le plan en un point je ne vois pas lequel
-
La projection orthogonale du point A(1;1;0)A(1;1;0)A(1;1;0) sur le plan PPP modifie quelle(s) coordonnée(s) ?
-
AAgnès quintil dernière édition par
la projection orthogonale du point A sur le plan modifie les coordonnées du vecteur i et le vecteur k
-
Si on note A′A'A′ le point d'impact, quelles sont ses coordonnées ?
-
AAgnès quintil dernière édition par
A' a pour coordonnée (0;1;0)
-
Non, c'est (−5;1;0)(-5;1;0)(−5;1;0)
-
AAgnès quintil dernière édition par
merci c'est pour la quel question j'ai suis me trompé sur les coordonnée
-
AAgnès quintil dernière édition par
j'ai trouvé mon erreur mais je sais pas c'est pour quelle question
-
C'est la réponse à la question 1 b).
-
AAgnès quintil dernière édition par
merci de m'aider pour l'exercice
-
AAgnès quintil dernière édition par
donc la réponse pour la question 1a) c'est parce que le vecteur i est un vecteur directeur car il est normal au coordonnée (1;1;0)
-
Oui, mais il faut que tu indiques tes calculs.
Pour la question 2, démontre que la droite correspondant au faisceau lumineux est parallèle au plan PPP.
Donc qu'un vecteur directeur de la droite est orthogonal à un vecteur normal du plan.
-
AAgnès quintil dernière édition par
je n'ai fait aucun calcul pour la question 1a j'ai juste regarder le schéma
-
AAgnès quintil dernière édition par
c'était quoi le calcul faire pour la question 1a
-
Pas de calcul à faire, il faut préciser que le point de coordonnées (1;1;0)(1;1;0)(1;1;0) appartient à un plan (à préciser) qui est orthogonal au plan PPP.
-
AAgnès quintil dernière édition par
donc j'ai juste a dire que les coordonnée (1;1;0) appartient au plan (vecteur i; vecteur j;vecteur k)
-
Non, c'est le plan (O,i→;j→)(O,\overrightarrow{i};\overrightarrow{j})(O,i;j)
-
AAgnès quintil dernière édition par
merci je sais pas pk j'ai rajoute le vecteur k alors que je ne l'ai pas mis sur ma feuille par contre j'avais oublié le O .
-
AAgnès quintil dernière édition par
je n'arrive pas à ce que vous me demander à la question 2
-
Cherche les coordonnées d'un vecteur directeur de la droite correspondant au faisceau lumineux.
-
AAgnès quintil dernière édition par
je ne vois pas le vecteur directeur a part si c'est le vecteur i
-
Tu as les coordonnées de deux points du faisceau (1;2;3)(1;2;3)(1;2;3) que tu peux appeler point BBB et (1;3;5)(1;3;5)(1;3;5) pour un point CCC.
Calcule les coordonnées du vecteur BC→\overrightarrow{BC}BC.
Tu choisis ensuite un vecteur normal au plan PPP, soit par exemple n→:(1;0;0)\overrightarrow{n}:(1;0;0)n:(1;0;0).
Puis tu calcules le produit scalaire des deux vecteurs.
-
AAgnès quintil dernière édition par
merci pour votre aide et j' ai réussi comprendre je le fais toute suite le calcul
-
AAgnès quintil dernière édition par
j'ai trouvé pour le vecteur BC (0;1;2) et le produit scalaire égale à 0
-
C'est correct, tu en déduis que le faisceau est parallèle au plan donc il n'éclaire pas la façade.
-
AAgnès quintil dernière édition par
merci beaucoup
-
AAgnès quintil dernière édition par
pour la question 3 , je dois faire quoi pour trouver les réel y et z
-
Pour la question 3, détermine l'équation paramétrique de la droite passant par les points de coordonnées (−1;−2;1)(-1;-2;1)(−1;−2;1) et (−5;1;6)(-5;1;6)(−5;1;6) puis tu détermines la valeur de yyy et zzz en utilisant le fait que le point de coordonnées (7;y;z)(7;y;z)(7;y;z) appartient à la droite.
-
AAgnès quintil dernière édition par
D(-1;-2;1) et E(-5;1;6) pour déterminer l'équation je dois determiner le vecteur DE et après faire le produit scalaire du vecteur DE fois les coordonnées (7;y;z)
-
Non,
Détermine les coordonnées du vecteur DE→\overrightarrow{DE}DE puis écris une équation paramétrique de la droite (DE)(DE)(DE).
-
AAgnès quintil dernière édition par
c'est quoi une équation paramétrique
-
AAgnès quintil dernière édition par
je trouve pour le vecteurs DE (-4;3;5)
-
Tu n'as pas un cours ?
Soit (d)(d)(d) la droite passant pas le point A(xA;yA;zA)A (x_A ; y_A ; z_A)A(xA;yA;zA) et de vecteur directeur u→:(a;b;c)\overrightarrow{u} : (a ; b ; c)u:(a;b;c).Le point M(x;y;z)M (x ; y ; z)M(x;y;z) appartient à la droite (d)(d)(d) signifie qu'il existe un nombre réel ttt tel que .
Les coordonnées de MMM vérifient donc le système suivant :
{x=at+xAy=bt+yAz=ct+zA\begin{cases} x=at+x_A \cr y=bt+y_A \cr z=ct+z_A \end{cases}⎩⎪⎪⎨⎪⎪⎧x=at+xAy=bt+yAz=ct+zA
Tu dois trouver :
{x=−4t−1y=3t−2z=5t+1\begin{cases} x=-4t-1 \cr y=3t-2 \cr z=5t+1 \end{cases}⎩⎪⎪⎨⎪⎪⎧x=−4t−1y=3t−2z=5t+1
Puis tu résous :
{7=−4t−1y=3t−2z=5t+1\begin{cases} 7=-4t-1 \cr y=3t-2 \cr z=5t+1 \end{cases}⎩⎪⎪⎨⎪⎪⎧7=−4t−1y=3t−2z=5t+1
Détermine la valeur de ttt puis yyy et zzz.
-
AAgnès quintil dernière édition par
non je n'ai pas ce cours
-
AAgnès quintil dernière édition par
j'ai trouvé t=-2 , y=-8 et z=-9
-
C'est la solution.
-
AAgnès quintil dernière édition par
Merci de m'avoir m'aider pour cet exercice
-
C'est bien car tu as suivi les conseils et réalisé les calculs.
J'espère que tu as tout compris.
-
mtschoon dernière édition par

Bonjour/Bonsoir
Seulement une réflexion.
L'énoncé laisse beaucoup de liberté sur la démarche, sans doute pour permettre aux élèves de prendre des initiatives
Le schéma donné n'est guère parlant...Au tout début, @Agnès-quintil indique :
"dans le repère (O; vecteur i ; vecteur j ; vecteur k )"
La nature du repère n'est pas indiquée (quelconque ou orthogonal ou orthonormé ) et il faut se référer au schéma joint...
Alors , on peut considérer que le schéma représente un repère orthonormé, mais il serait bon que @Agnès-quintil l'indique avant d'utiliser des explications avec projection orthogonale, normale, produit scalaire,...Bien sûr, l'exercice peut être fait avec un repère quelconque non orthonormé, mais les explications seraient différentes...
-
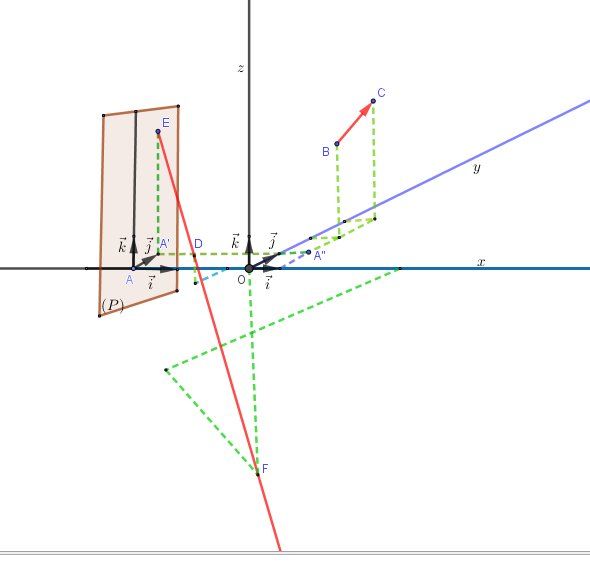
mtschoon dernière édition par mtschoon

Un schéma (tout à fait approximatif) , vu sous un angle différent du schéma de l'énoncé , pour donner un autre éclairage.
Notations :
Vu que l'énoncé a appelé AA A le point de coordonnées (−5,0,0)(-5,0,0)(−5,0,0), le point de coordonnées (1,1,0)(1,1,0)(1,1,0) est appelé A′′A''A′′
Le point FFF est le point de coordonnées (7,−8,−9)(7,-8,-9)(7,−8,−9)