Dm de maths terminale sur les limites de fonctions

Bonjour,
je suis en terminale spécialité maths et j’ai du mal avec cet exercice. Je suis bloquée à la question 2 car on a une forme indéterminée et lorsque je la factorise pour la lever j’ai toujours une FI ?
La fonction est : f(x)=(x2+x+1)/(x2+2x-3)
Questions:
1/trouver l’ensemble de définition
2/les limites de la fonction aux bornes de l’ensemble de définition
3/une équation de chaque asymptote éventuelle
4/le tableau de variation
Voici ce que je trouve lorsque je factorise :
(1+1/x+1/x)/(1+2/x-3/x)
Merci par avance, Lola.

@Mimisss12 , bonsoir,
Je suppose que tu as voulu écrire
$f(x)=x2+x+1x2+2x−3f(x)=\dfrac{x^2+x+1}{x^2+2x-3}$

Pour l'ensemble de définition :
$Df=]−∞,−3[∪]−3,1[∪]1,+∞[D_f=]-\infty,-3[\cup]-3,1[\cup]1,+\infty[$

Pour + $∞\infty$ et - $∞\infty$ , en prenant les termes de plus fort degré (ou en mettant x^2 en facteur) tu dois trouver $1$

Pour les limites à -3 et 1, tu peux factoriser le dénominateur

$f(x)=x2+x+1(x−1)(x+3)f(x)=\dfrac{x^2+x+1}{(x-1)(x+3)}$

Je t'indique le cas de 1

Lorsque x tend vers $1$ , le numérateur tend vers 3
le dénominateur tend vers $0$
Tu dois distinguer la limite à gauche et la limite à droite.

Lorsque $x$ tend vers 1 par valeurs supérieures à $1$ , $(x - 1)$ tend vers $0^+$ , $(x + 3)$ tend vers $4$ donc le produit $(x - 1) (x + 3)$ tend vers $0^+$
Le quotient tend vers $+∞+\infty$

$lim⁡x→1,x>1f(x)=+∞\displaystyle \lim_{x\to 1, x\gt 1} f(x)=+\infty$

En raisonnant de la même façon, tu dois trouver, lorsque $x$ tend vers $1$ par valeurs inférieures à $1$ :
$lim⁡x→1,x<1f(x)=−∞\displaystyle \lim_{x\to 1, x\lt 1} f(x)=-\infty$

Même principe pour -3

$lim⁡x→−3,x>−3f(x)=−∞\displaystyle \lim_{x\to -3, x\gt -3} f(x)=-\infty$

$lim⁡x→−3,x<−3f(x)=+∞\displaystyle \lim_{x\to -3, x\lt -3} f(x)=+\infty$

Travailles tout ça de près.

@mtschoon
Merci beaucoup
J’ai oublié de marquer l’ensemble de définition que j’avais trouvé, c’était R{-3;1}
Je pense avoir compris vos remarques, merci pour votre aide.

@Mimisss12 ,

Ton ensemble de définition est bon.

J'espère que ça ira pour tes limites, mais reposte si tu as besoin de précision.

@mtschoon
Bonjour !
J’ai une question à propos de la question 3 sur les asymptotes. La limite de f(x) c’est l’infinie donc l’asymptote sera verticale ?

@Mimisss12 , bojour,

Oui, tu as deux asymptotes "verticales" d'équation $x = - 3$ et $x = 1$
Tu as aussi l'asymptôte "horizontale" d'équation $y = 1$ (pour x tendant vers + $∞\infty$ et - $∞\infty$

@Mimisss12
Illustration graphique si besoin.
Les trois asymptotes sont en rouge.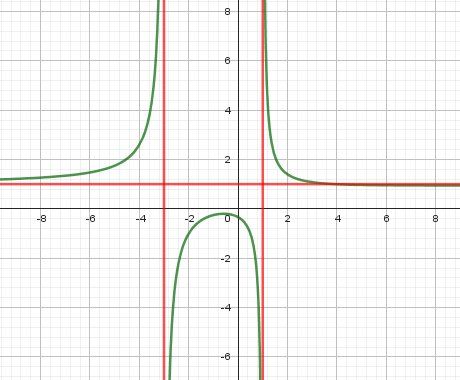

Bon travail

@mtschoon
Ha super merci, j’étais en train de le faire pour mieux visualiser.
Cependant je reviens à la question précédente, pouvez-vous me dire si c’est juste pour -3 ?
lim (x-1)=4
x->-3-
lim (x+3)=0+
x->-3-
Donc par produit on a 0+ et par quotient on +♾
C’est la que ça me gêne, j’aurai dit lim (x+3)=0-
Mais alors par quotient on aurait -♾ alors que vous aviez dit que c’était +♾ ?

@Mimisss12 je me suis pas relu, c’est -4 pour lim (x-1)

@Mimisss12

Tu as une erreur dans un signe.

Lorsque $x$ tend vers $- 3$ (que ça soit par valeurs supérieures ou inférieures à $- 3$ ), $(x - 1)$ tend vers $- 3 - 1 = - 4$

@mtschoon
Ok merci. Donc lim (x+3)=0+ ?
x->-3-
Donc par produit on a 0+ et par quotient on a +♾ ?

@Mimisss12 ,

Non,
Lorsque x tend vers $3^{-}$ , $x<−3x\lt -3$ donc $x+3<0x+3\lt 0$
donc $x + 3$ tend vers $0^-$

@mtschoon
D’accord merci !

De rien @Mimisss12 , fais bien attention aux signes.