calculer des probabilités

bonjour , j'ai besoin de votre aide pour cette exercice merci .
Avant le début des travaux de construction d'une autoroute , une équipe d'archéologie préventive procède à des sondages successifs en des points régulièrement espacés sur le terrain.
Lorsque le n-ième sondage donne lieu à la découverte des vestiges , il est dit positif.
L'événement :"le n-ième sondage est positif " est noté Vn , on note Pn la probabilité de l'événement Vn.
L'expérience acquises au cours de ce type d'investigation permet de prévoir que:

si un sondage est positif , le suivant a une probabilité égale à 0.6 d'être aussi positif.
si un sondage est négatif , le suivant a une probabilité égale à 0.9 d'être négatif.
on suppose que le premier sondage est positif, c'est à dire p1=1.
1)calculer les probabilité des événement suivants:
A: "les 2-ième et 3-ième sondage sont positif"
B: " les 2-ième et 3-ième sondage sont négatif"
2)calculer la probabilité p3 pour que le 3-ième sondage soit positif ?
3)n est désigné un entier naturel supérieur ou égal à 2.
compléter l'arbre ci dessous en fonction des données de l'énoncé :

Pour tout entier naturel n non nul, établir que Pn+1=0.5Pn+0.1.
5)on note u la suite définie , pour tout entier naturel n non nul , par Un=Pn-0.2.
a) Démontrer que u est une suite géométrique . En préciser le premier terme et la raison.
b) Exprimer Pn en fonction de n
c) calculer la limite , quand n tend vers +00, de la probabilité de Pn.

@Agnès-quintil , bonjour,

Tu ne dis pas précisément où se situe ta difficulté.

Je vois que tu as fait un arbre incomplet.
Je te joins l'arbre avec les données.

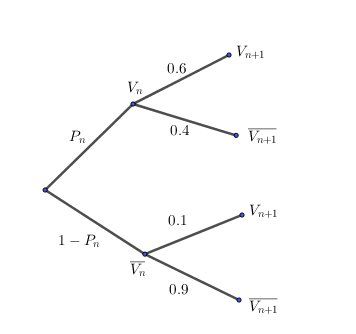
Reposte si tu as d'autres questions.

@mtschoon bonjour, merci pour mon aide . Ma difficulté est tout l exercice car je ne l ai pas compris

@Agnès-quintil , pour t'éclairer ( peut-être ?) , je t'ai fait un arbre pour les deux premières questions , relatif au 2ème et 3ème sondage.

Essaie de comprendre le principe (en regardant aussi les exercices que tu as fait en cours) .

La branche en pointillés n'est pas indispensable, vu qu'elle correspond à une probabilité nulle.
Tu peux ne pas la mettre.
J'espère que tu connais la notation : la barre au dessus d'un événement veut dire "événement contraire"

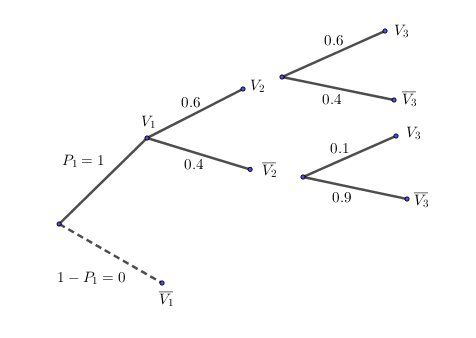
Lorsque tu auras compris le principe, fais les calculs avec cet arbre pour les deux premières questions et si le souhaites, donne tes réponses ( à la 1 ) et à la 2 ) pour vérification et t'assurer que tu as bien compris la démarche.

Bonsoir,
Pour la question 1
l evenement A a pour probabilité 0.36 et pareil pour l evenement B .
Merci

Bonsoir,
Pour la question 2 je trouve 0,40
Merci pour votre aide

@Agnès-quintil Bonsoir,

Les réponses sont correctes.

@Agnès-quintil Oui, c'est bon.

Maintenant, avec l'arbre fait pour la question 3 ), si tu l'as bien compris, tu dois pouvoir faire les calculs de $P_{n+1}$ en fonction de $P_n$ .
Reposte si besoin.

Bonjour,
Je n arrive pas a exprimer Pn+1 en fonction de Pn
Merci pour votre aide

@Agnès-quintil , bonjour,

C'est la même méthode que pour la question 1 ) et la question 2 )

Avec l'arbre relatif à la troisième question (que je t'ai complété) , deux branches (qui se terminent à $V_{n+1}$ )sont à utiliser

$p(Vn+1)=0.6p(Vn)+0.1p(Vn‾)p(V_{n+1})=0.6p(V_n)+0.1p(\overline{V_n})$
c 'est à dire :
$p_{n+1}=0.6p_n+0.1(1-p_n)$
Tu termines le calcul.

Merci j ai trouvé ce que la question demander

@Agnès-quintil , c'est bien.

Tu as du voir de quoi il s'agit pour terminer l'exercice.

La suite $U_n)$ proposée est une suite auxiliaire utilisée pour trouver l'expression de $P_n$ en fonction de $n$ et sa limite.

Pour vérification, je t'indique ce que tu dois trouver pour $U_n)$

$U_n)$ est la suite géométrique de raison $q = 0.5$ et de premier terme $U_1=P_1-0.2=1-0.2=0.8$

J'espère que tu vas y arriver.

Merci pour votre aide

De rien @Agnès-quintil
Tu peux donner l'expression de $P_n$ et la limite, si tu souhaites une vérification.

Je n arrive pas a demontrer que c est une suite geometrique

Car je trouve 0,5(Pn+1)

@Agnès-quintil , lorsque tu auras terminé ton exercice avec aide, je te conseille de le refaire seule pour être sûre de le maîtriser et pouvoir progresser.

$U_n=P_n-0.2$
$U_{n+1}=P_{n+1}-0.2$
Tu remplaces $P_{n+1}$ par l'expression trouvée.
$U_{n+1}=0.5P_n+0.1-0.2$
$U_{n+1}=0.5P_n-0.1$
$U_{n+1}=0.5(P_n-0.2)$
$U_{n+1}=0.5U_n$
d'où la réponse proposée.

Je comprend mieux mon erreur je suis parti sur Un+1/Un

Tu aurais pu y arriver avec le quotient.

$Un+1Un=Pn+1−0.2Pn−0.2=0.5Pn+0.1−0.2Pn−0.2\dfrac{U_{n+1}}{U_n}=\dfrac{P_{n+1}-0.2}{P_n-0.2}=\dfrac{0.5P_n+0.1-0.2}{P_n-0.2}$

$Un+1Un=0.5Pn−0.1Pn−0.2\dfrac{U_{n+1}}{U_n}=\dfrac{0.5P_n-0.1}{P_n-0.2}$

$Un+1Un=0.5(Pn−0.2)Pn−0.2\dfrac{U_{n+1}}{U_n}=\dfrac{0.5(P_n-0.2)}{P_n-0.2}$

$Un+1Un=0.5\dfrac{U_{n+1}}{U_n}=0.5$

CQFD

Ah ok . J ai trouver pour Pn =0,5 a la puissance n + 0,16

Tu dois avoir fait une confusion.

$Un=U1×qn−1U_n=U_1\times q^{n-1}$ (voir cours sur suite géométrique, fais attention car le premier terme est $U_1$ , pas $U_0$ )

$Un=0.8×(0.5)n−1U_n=0.8\times (0.5)^{n-1}$

$P_n=U_n+0.2$

donc :

$Pn=0.8×0.5n−1+0.2P_n=0.8\times 0.5^{n-1}+0.2$

(0.8 et 0.2 ne sont pas multipliés)

Ah ok . Merci je repare mon erreur et je calcule la limite

J ai trouvé que la limite en plus l infini de Pn est égale a 0,2

@Agnès-quintil ,

Oui, la limite que tu as trouvée est bonne.

@mtschoon merci pour votre aide . Ca m a beaucoup aidé

De rien @Agnès-quintil , c'était avec plaisir !

Comme je te l'ai déjà dit :
Un conseil.
Prends une page blanche et seulement l'énoncé, et refais l'exercice seule, pour t'entraîner.
Cela te prendra un peu de temps, mais ça en vaudra la peine, pour faire des progrès.

Bon travail !

Merci je le refaire

C'est très bien @Agnès-quintil .