Aide dérivation devoir maison
-
Hhiba_mrcnn dernière édition par
L'objectif de cette activité est de découvrir une méthode de construction géométrique de la tangente en un point de la parabole d'équation y = x?
Le plan est muni d'un repère.
On désigne par P la courbe d'équation y = x?- Conjectures
a) En utilisant le logiciel GeoGebra, créer la courbe P.
b) Tracer la tangente en un point quelconque de la courbe P.
c) Conjecturer une propriété commune à chacune des tangentes et qui permette de construire la tangente à la courbe P en un de ses points.
d) Joindre une capture d'écran à votre devoir maison. - Démonstration
Démontrer la propriété conjecturée.
31 - Application
Mettre en œuvre la propriété obtenue pour construire ci-contre (sans faire un seul calcul) la tangente
a
courbe P au point
A
J’arrive pas à mettre une photo
- Conjectures
-
@hiba_mrcnn Bonjour (Marque de politesse à ne pas oublier !!)
Indique tes éléments de réponse et la question qui te pose problème.
-
Hhiba_mrcnn dernière édition par
@Noemi
Ah excuser moi j’ai pas réussi à le faire
Merci
-
Tu n'as pas réussi à créer la courbe sur Géogébra ?
Est-ce bien y=x2y=x^2y=x2 ?
-
mtschoon dernière édition par mtschoon

Bonjour,
@hiba_mrcnn , vu que tu parles de parabole, je suppose que ton "?" veut dire "2" et qu'il s'agit de y=x2y=x^2y=x2
Si tu enregistres un fichier de Geogebra il a pour extension ggb
Tu peux l'appeler par exemple "tangente.ggb"
Tu ne peux pas mettre directement ce fichier sur le site avec "Envoyer une image" car ce n'est pas un fichier image.Il faut que tu le transformes en fichier image, par exemple, "tangente.jpg"
Ensuite, en cliquant sur l'icône "envoyer une image", tu vas à "tangente.jpg" contenu dans ton disque dur, tu cliques et l'image arrive dans ton message à l'écran.Exemple :
-
mtschoon dernière édition par

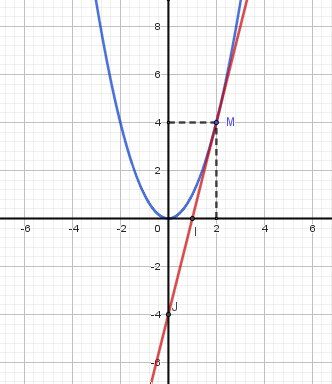
@hiba_mrcnn , à tout hasard, je t'indique les coordonnées des points du schéma joint,
M(a,a2)M(a,a^2)M(a,a2) pour a≠0a\ne 0a=0.
Ici : a=2a=2a=2
Tangente (T)(T)(T) en rouge : y=f′(a)(x−a)+f(a)y=f'(a)(x-a)+f(a)y=f′(a)(x−a)+f(a)
c'est à dire : y=2a(x−a)+a2y=2a(x-a)+a^2y=2a(x−a)+a2
Après calculs : y=2ax−a2y=2ax-a^2y=2ax−a2Point III (intersection de (T)(T)(T) avec l'axe des abscisses ) : y=0y=0y=0 d'où x=a2x=\dfrac{a}{2}x=2a donc I(a2,0)I(\dfrac{a}{2},0)I(2a,0)
Point JJJ (intersection de (T)(T)(T) avec l'axe des ordonnées ) : x=0x=0x=0 d'où
y=−a2y=-a^2y=−a2 donc J(0,−a2)J(0,-a^2)J(0,−a2)
-
Hhiba_mrcnn dernière édition par
Jsp comment insérer une image
-
Tu as eu l'indication pour transmettre une image dans un précédent message de mtschoon.
-
Hhiba_mrcnn dernière édition par Noemi
Lien vers l'énoncé complet de l'exercice supprimé par la modération du site.
-
Attention,
Le scan ou un lien de l'énoncé de l'exercice est interdit sur ce forum. Seuls les scans de schémas, graphiques ou figures sont autorisés.
Écris l'énoncé, tes éléments de réponse et indique la question qui te pose problème. Tu obtiendras alors des pistes de résolution.Le scan va être supprimé par la modération du site.
-
Hhiba_mrcnn dernière édition par
Oui mais je n’arrive ps à insérer la figure sinon
-
Pour transmettre la figure, utilise l'icône image.
Pour le schéma, tu as du obtenir obtenir une figure identique à celle postée par mtschoon.
Passe à la conjecture.
-
Hhiba_mrcnn dernière édition par
Ce message a été supprimé !
-
Hhiba_mrcnn dernière édition par
Sa ne marche ps
-
Tu dois coller la photo dans la partie "(url de l'image)".
-
Hhiba_mrcnn dernière édition par
Ce message a été supprimé !
-
Hhiba_mrcnn dernière édition par
Ce message a été supprimé !
-
Hhiba_mrcnn dernière édition par
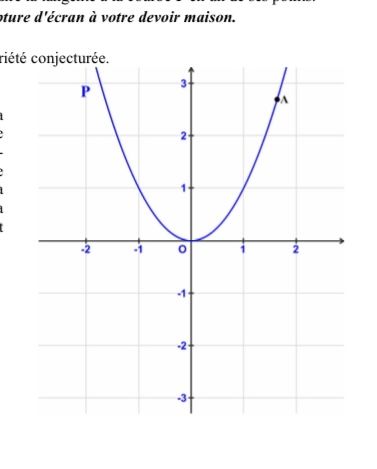
La courbe dans l’énoncé représente sa
Énoncer
L'objectif de cette activité est de découvrir une méthode de construction géométrique de la tangente en un point de la parabole d'équation y = x?
Le plan est muni d'un repère.
On désigne par P la courbe d'équation y =- Conjectures
a) En utilisant le logiciel GeoGebra, créer la courbe P.
b) Tracer la tangente en un point quelconque de la courbe P.
c) Conjecturer une propriété commune à chacune des tangentes et qui permette de construire la tangente à la courbe P en un de ses points.
d) Joindre une capture d'écran à votre devoir maison. - Démonstration
Démontrer la propriété conjecturée. - Application
Mettre en œuvre la propriété obtenue pour construire c1-contre sans faire un seul calcul) la tangente à la courbe P au point
A
- Conjectures
-
Hhiba_mrcnn dernière édition par
Peut tu me citez les étapes s’il te plaît
-
mtschoon dernière édition par

@hiba_mrcnn ,
Je pense que tu peux t'inspirer de la réponse que je t'ai donnée précédemment.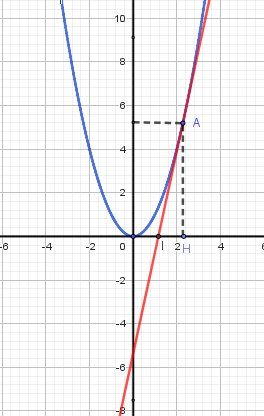
Soit AAA un point quelconque de la parabole (autre que OOO), de coordonnées (a,a2)(a,a^2)(a,a2)
Soit HHH projeté de AAA sur l'axe des abscisses donc H(a,0)H(a,0)H(a,0)Conjecture d'une propriété commune :
En traçant plusieurs tangentes , tu peux constater qu'elles coupent toutes l'axe de abscisses en un point III milieu de [OH]Pour le démontrer regarde ma première réponse :
Tu cherches l'équation de la tangente en AAA
Tu cherches l'abscisse du point d'intersection III de la tangente avec l'axe des abscisses et tu dois trouver I(a2,0)I(\dfrac{a}{2},0)I(2a,0), d'où la réponse souhaitée.Conséquence pour la construction d'une tangente en un point AAA :
On place ce point AAA sur la parabole.
On place son projeté HHH sur l'axe des abscisses
On place le milieu III de [OH][OH][OH]
Sans aucun calcul, il ne reste qu'à tracer la droite passant par AAA et par III, qui est la tangente.Bons calculs et bonnes réflexions
-
Hhiba_mrcnn dernière édition par
Ce message a été supprimé !
-
Hhiba_mrcnn dernière édition par
Peut tu me partager le fichier svp ?
-
mtschoon dernière édition par mtschoon

@hiba_mrcnn ,
J'espère que tu as bien compris la démarche et je pense que tu as tout ce qu'il faut pour ton travail.
Bien sûr, reposte si quelque chose n'est pas clair.
-
Hhiba_mrcnn dernière édition par
D’accord merci, les étapes de Geogebra j’ai fait le début mais pas la suite
-
mtschoon dernière édition par mtschoon

@hiba_mrcnn ,
Reparde la réponse que je t'ai donné hier à 18 heures.
Il y a tout ce qu'il faut.
-
Hhiba_mrcnn dernière édition par
Donc c’était sa le dm qu’il fallait faire ?
-
mtschoon dernière édition par mtschoon

Oui.
Le but de l'exercice est de pouvoir construire une tangente à la parabole sans faire de calcul.
C'est ce que j'ai indiqué dans la conclusion :
"Conséquence pour la construction d'une tangente en un point A "Revois tout ça de près.