Equation paramétrique du second degré avec une valeur absolue

[hibaaaa]

Bonjour, j'ai besoin d'aide, merci ! Bonjour !!
j'ai une petite question, alors je bloque sur comment calculer ALGEBRIQUEMENT
x²-4|x|+3=m
enfin si je sais que je dois utiliser le discriminant mais pour la valeur absolue je fais quoi ??? une disjonction des cas?
merci !

[Noemi]

@hibaaaa Bonjour,

Oui pour une disjonction des cas.

[hibaaaa]

@Noemi d'accord merci beaucoup

[Black-Jack]

Bonjour,

Autre option :

Remarquer que la fonction x| --> x² - 4|x| + 3 - m est paire ...
qui permet de n'étudier que pour x dans R+ et profiter de la symétrie due à la parité de la fonction pour étendre les conclusions sur R

[mtschoon]

Bonjour tout le monde,

@hibaaaa , je trouve ta question peu précise.
On comprend qu'il faut calculer ALGEBRIQUEMENT, c'est à dire "non graphiquement", je suppose.
Mais , ça veut dire quoi "calculer"....

Tu as une équation apparemment d'inconnue $x$ :
$x^2-4|x|+3=m$
Tu ne dis rien sur $m$ ; ce doit être un paramètre réel.

Alors, la question est-elle de déterminer, suivant $m$, les expressions des solutions ou seulement de donner le nombre de solutions ?
Merci de le préciser.

En ce qui concerne la disjonction des cas, bien sûr :

1er cas (cas "limite") : pour $x=0$, $|x|=0$,
l'équation se se ramène à $3=m$

2ème cas : pour $x>0$, $|x|=x$ :
l'équation se se ramène à $x^2-4x+3=m$

2ème cas : pour $x<0$, $|x|=-x$ :
l'équation se se ramène à $x^2+4x+3=m$

[mtschoon]

@hibaaaa ,
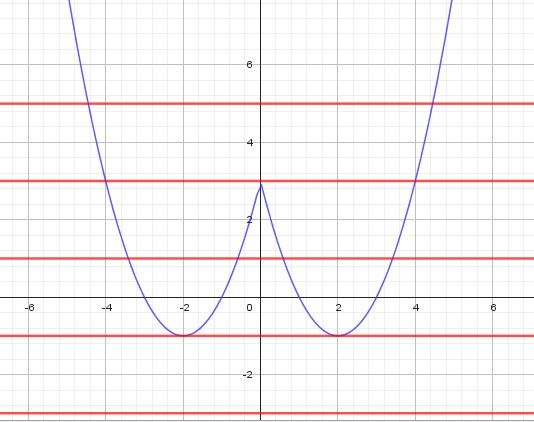
Je te mets un graphique ( que tu peux obtenir avec ta calculette) .
Ce n'est pas à utiliser vu que tu dois traiter le problème algébriquement, mais pour comprendre la démarche.

La représentation de $f$ définie par $f(x)=x^2-4|x|+3$ est la courbe en bleu

La représentation de $y=m$ pour quelques valeurs de $m$ : $m=5,3,1{,}_{-}1,-3$ est composée des droites en rouge.

L'équation à traiter est $f(x)=m$