Problème de fonction exponentielle

Bonjour, j'aimerais votre aide pour un problème de math que vous trouverez ci dessous, je vous remercie d'avance :

Au 1er janvier 2022 la population d'un pays est estimée à 20 000 000 d'habitants Elle augmente de 1% par an

On la modélise par une suite en notant Un le nombre d'habitants dans ce pays au 1er janvier de l'année (2022+ n), pour tout entier naturel n

a) Calculer le nombre d'habitants prévu au 1er janvier 2023

b) Calculer U2 et interpréter ce résultat

c) Pour tout entier naturel n, exprimer Un+1 en fonction de Un Quelle est la nature de la suite (Un) ?

d) Pour tout entier naturel n, exprimer Un en fonction de n

e) Combien d'habitants peut-on prévoir dans ce pays au 1er janvier 2056 selon ce modèle ?

(arrondir au millier près)

On décide de prolonger la suite (Un) en une fonction f definie sur R par

f(t) = k a^t

telle que pour tout entier naturel n, f(n) = Un

a) Sachant que f(0) = U0 = 20 000 000 et que f(1) = U1 , Déterminer les valeurs des réels k et a

b) Déterminer, selon ce modèle, le nombre d'habitants dans ce pays au 1er septembre 2023

(arrondir au millier près)

c) Calculer f(8,25) au millier près, et interpréter le résultat

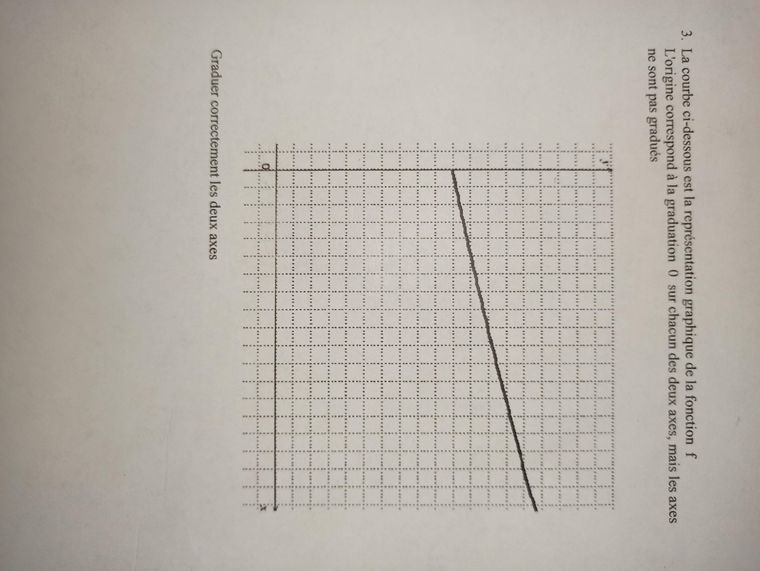
La courbe ci-dessous est la représentation graphique de la fonction f L'origine correspond à la graduation 0 sur chacun des deux axes, mais les axes ne sont pas gradués

(Pour le graphique je ne malheureusement pas l'envoi, sous peine de voir mon envoie supprimer)

Graduer correctement les deux axes

@Greeny Bonjour,

Indique tes éléments de réponse et la question qui te pose problème.

Tu peux transmettre le graphique, ceux ne sont que les énoncés et réponses qui doivent être écrits, les scans de graphiques, schémas ou figures sont autorisés.

Bonjour,
Si besoin, je t'indique la marche à suivre pour débuter ton exercice,

1 ) a)
$U_0=20000000$
$U_1=U_0+0.01U_0=1.01U_0$ Tu comptes

1 ) b)
$U_2=1.01U_1=(1.01)^2U_0$ Tu comptes

1 )c)
$U_{n+1}=1.01U_n$
$U_n)$ suite géométrique de raison $q = 1.01$ et de premier terme $U_0$

1 )d)
Regarde ton cours sur les suites géométriques.
$U_n=U_0q^n$ Tu explicites

1 )e)
2056=2022+34$
Tu calcules $U_{34}$

Lorsque tu auras fait cette partie 1) , essaie de poursuivre et reposte si besoin.

@mtschoon Très bien merci

De rien @Greeny ,
Comme déjà indiqué, après avoir fait la question 1), tu peux demander si tu as besoin de pistes pour la question 2).

@mtschoon Bonjour, j'ai terminé la première partie mais je trouve la seconde partie impossible, pouvez vous m'éclairer ? Merci

@Greeny Bonjour,

Pour la question 2. a) tu as à résoudre le système défini à partir de
$f (0) = 20000000$ et $f (1) = 20200000$
soit
$ka^0=20000000$
$ka^1=20200000$

Bonjour,

@Greeny , la seconde question est une généralisation de la première à toute valeur de $t$ réelle.

Comme te l'a dit Noemi,

$f(t)=ka^t$ pour tout $t$ réel

$f(0)=ka^0=U_0$ .
Vu que $a^0=1$
$k=U_0=200 000 000$

donc $f(t)=20 000 000\ a^t$

$f(1)=U_1=20 000 000\ a^1$ .
Vu que $a^1=a$
$f(1)=U_1=20 000 000\ a$
Tu as calculé $U_1$ à la première question, donc tu peux en déduire $a$

Sauf erreur, tu dois trouver :
$f(t)=20 000 000(1.01)^t$

Reposte si tu n'arrives pas à poursuivre
(Pense à raisonner en mois)

@mtschoon Bonjour, pour la question b, faut il calculer 20000000(1.01)^1.75 ? Merci

@Greeny

Pourquoi 1,75 ?

@Noemi Enfaite je me suis dis qu'il fallait mettre en mois donc 1÷12 = 0,0833333333
0,0833333333*9 (pour le mois de septembre) = 0,75 et après on rajoute 1 donc 1,75
C'est farfelu mais j'ai trouver que ça

@Greeny

C'est la bonne démarche, mais au 1 septembre, seulement 8 mois se sont passés.

@Noemi Effectivement merci

@Noemi La réponse est donc 20000000(1,01)^1.6666666 = 20334443,2

Bonjour,

@Greeny , je ne comprends pas ta proposition

$12$ mois = $1$ an
$1$ mois = $112\dfrac{1}{12}$ an
$8$ mois = $812\dfrac{8}{12}$ an= $23\dfrac{2}{3}$ an

Tu dois donc calculer , pour la question 2 ) b ) $20000000(1,01)2320000000(1,01)^\dfrac{2}{3}$

@Noemi Ensuite pour la question c, je dois donc faire 20000000(1,01)^8,25 = 21711075,1 ?
Mais il faut que j'interprète ce résultat, ça signifie quoi ?

@Greeny
Piste pour la 2 ) c)

C'est bien $20000000(1,01)^{8,25}$ qu'il faut calculer.

$8, 25$ ans = $8$ ans + $14\dfrac{1}{4}$ an= $8$ ans + $3$ mois

A partir de 01/01/ 2022, tu comptes quelle sera la date après $8$ ans + $3$ mois.

@mtschoon Ok, je comprends merci

@Greeny ,

J'espère que pour la date, tu as trouvé 01/04/2030

@Greeny
N'oublie pas, pour le nombre d'habitants, d'arrondir les résultats au millier près.

@Noemi ok

@Noemi
Voici donc le graphique

@Noemi J'imagine que pour le graphique x = le temps et y = le nombre d'habitants

@Greeny

Oui,

Place le premier point (2022 ; 20000000) puis détermine l'échelle sur l'axe des ordonnées.

Puis à partir d'un autre point tu détermines l'échelle sur l'axe des abscisses.

@Noemi ok merci

@Greeny

Indique tes solutions, si tu souhaites une vérification.

@Noemi ok

@Noemi J'ai pas vraiment de technique pour trouver l'échelle, c'est un peu compliqué

@Greeny

Le premier point à l'abscisse 0, tu notes 2022 et l'ordonnée 20000000.
Tu comptes ensuite le nombre de graduation de 0 à 20000000, puis tu détermines l'échelle de l'ordonnée.

@Noemi Ok merci