Bonjour j’aurais besoin d’aide avec cette fonction merci
-
Ss 1 dernière édition par Noemi
Scan supprimé par la modération du site.
-
@s-1 Bonjour,
Le scan ou un lien de l'énoncé de l'exercice est interdit sur ce forum. Seuls les scans de schémas, graphiques ou figures sont autorisés.
Écris l'énoncé, tes éléments de réponse et indique la question qui te pose problème. Tu obtiendras alors des pistes de résolution.Le scan va être supprimé par la modération du site.
-
Ss 1 dernière édition par
@Noemi (Je n'ai pas encore commencer l'exercice)
Soit f la fonction définie sur R par: f(x) = - x ^ 3 + 3x + 18
- Étudier le sens de variation de f.
- Déterminer le signe de f sur ]-?; 1].
3.a. Vérifier que f(3) = 0 .
b. Déterminer le signe de f(x) sur [1; +?[.
-
Il serait bien de terminer les autres exercices avant d'en proposer un de plus.
- Calcule la dérivée et étudie son signe.
-
mtschoon dernière édition par mtschoon

Bonjour,
@s-1 , j'espère qu'en deux jours, tu as fini tes autres exercices.
Je te mets quelques indications pour commencer celui-ci.
f(x)=−x3+3x+18f(x)=-x^3+3x+18f(x)=−x3+3x+18
fff est définie, dérivable sur RRRRegarde ton cours pour les formules de dérivées.
f′(x)=−3x2+3=−3(x2−1)=−3(x−1)(x+1)f'(x)=-3x^2+3=-3(x^2-1)=-3(x-1)(x+1)f′(x)=−3x2+3=−3(x2−1)=−3(x−1)(x+1)Le signe de f′(x)f'(x)f′(x) est le signe du produit de ces 3 facteurs et tu en déduis le sens de variation de la fonction fff.
Je te mets un tableau récapitulatif, mais tu peux le séparer en deux tableaux (un pour le signe de f′(x)f'(x)f′(x) et un pour le sens de variation de fff).
J'ai indiqué les limites en −∞-\infty−∞ et +∞+\infty+∞, mais j'ignore si tu les as vues en cours.
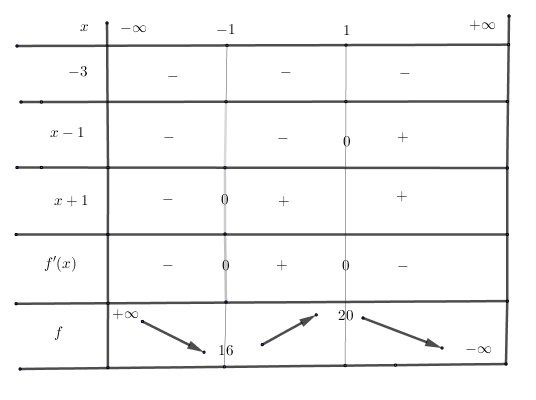
Etudie cela de près et essaie de poursuivre.
Reposte si besoin.