produit scalaire niveau première
-
Hhiba_mrcnn dernière édition par
Bonjour est-ce que quelqu’un pourrait m’aider à calculer AB • AC
Merci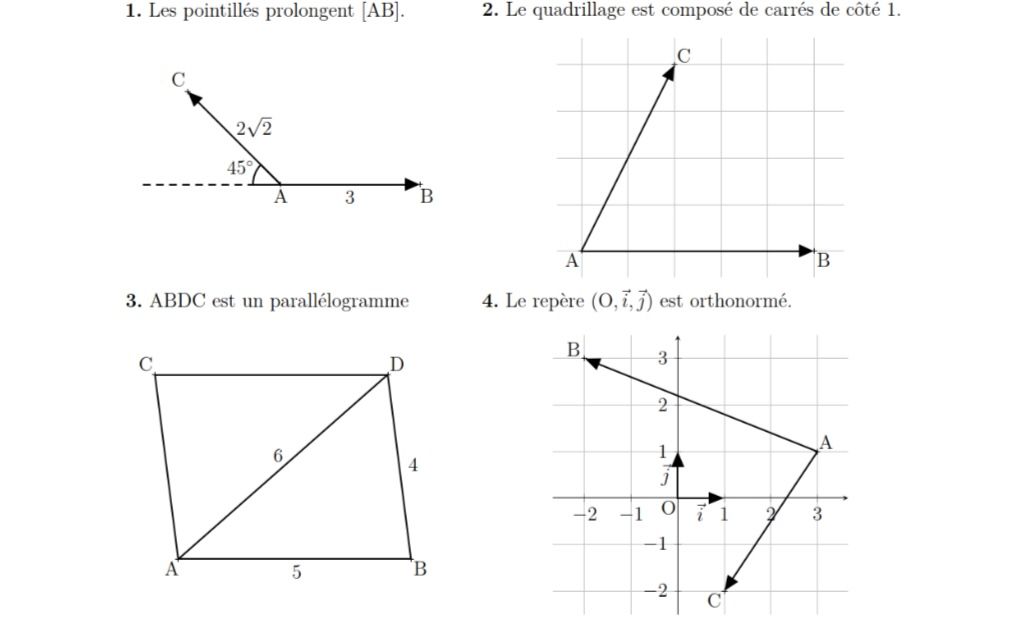
-
@hiba_mrcnn Bonjour,
Tu aurais du mettre en scan que les schémas et écrire l'indication pour chaque schéma afin de respecter le règlement du forum.
Indique tes éléments de réponse et la question ou figure qui te pose problème.
-
mtschoon dernière édition par mtschoon

Bonjour,
@hiba_mrcnn , une prochaine fois , il faudra faire ce que t'a indiqué @Noemi (modératrice) pour respecter les consignes du forum.
@Noemi a dit dans produit scalaire niveau première :
Tu aurais du mettre en scan que les schémas et écrire l'indication pour chaque schéma afin de respecter le règlement du forum.
Si j'ai bien compris, dans chaque question , tu dois calculer AB→.AC→\overrightarrow{AB}.\overrightarrow{AC}AB.AC
Si tu as besoin, je te mets une piste par question.
1 ) Tu utilises la définition du produit scalaire .
Tu calcules AB×AC×cos(180°−45°)AB\times AC\times cos(180°-45°)AB×AC×cos(180°−45°)2 ) Tu projettes orthogonalement le point CCC sur (AB)(AB)(AB) ce qui te donne un point HHH et tu utilises le théorème de la projection (et tu comptes les carreaux).
Tu calcules AB×AHAB\times AHAB×AH3 ) Par exemple,
AB→.AC→=−BA→.BD→\overrightarrow{AB}.\overrightarrow{AC}=-\overrightarrow{BA}.\overrightarrow{BD}AB.AC=−BA.BDAvec la formule d'Al-Kashi, dans le triangle ABDABDABD, tu trouves cosABD^cos\widehat{ABD} cosABD puis tu termines le calcul en utilisant la définition du produit scalaire.
4 ) Tu calcules les coordonnées de AB→\overrightarrow{AB}AB et AC→\overrightarrow{AC}AC puis tu appliques la formule du produit scalaire XX′+YY′XX'+YY'XX′+YY′
Bons calculs.