calculer les coordonnées d'un point inconnu en utilisant le cercle trigonométrique

[emma12]

Bonjour, je veux calculer les coordonnées du point comme indiqué sur le schéma en utilisant la trigonométrie, (sachant que je ne connais aucune information concernant ce point)

[Noemi]

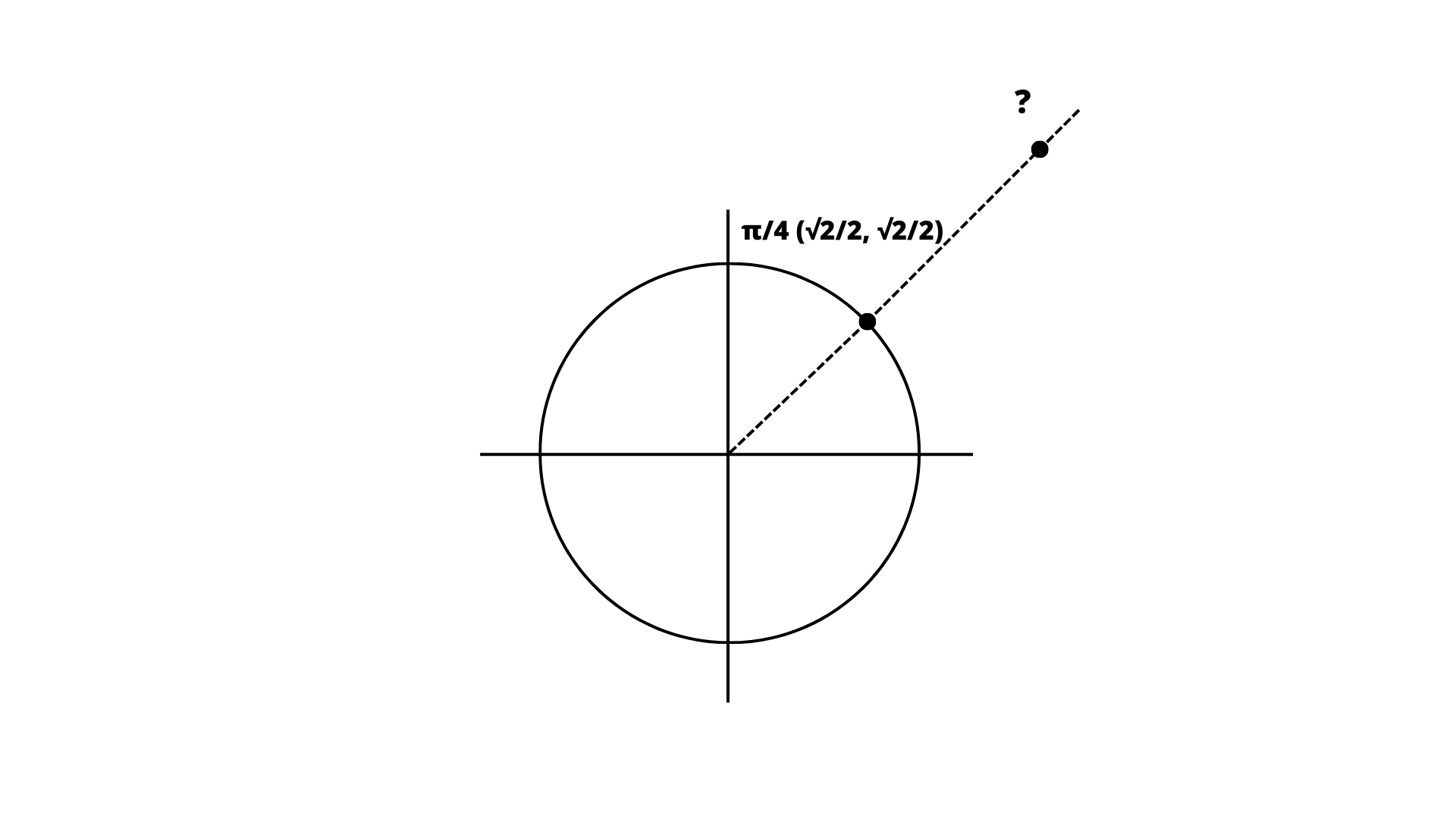
@emma12 Bonjour,

Le point est sur la droite d'équation $y=x$, donc ....

[emma12]

@Noemi Bonjour, donc quoi? j'ai pas compris

[Noemi]

@emma12

Les coordonnées du point peuvent s'écrire sous la forme $(a\frac{\sqrt{2}}{2};a\frac{\sqrt{2}}{2})$ avec $a$ un réel.

[mtschoon]

Bonjour,

@Noemi a dit dans calculer les coordonnées d'un point inconnu en utilisant le cercle trigonométrique :

@emma12
Les coordonnées du point peuvent s'écrire sous la forme $(a\frac{\sqrt{2}}{2};a\frac{\sqrt{2}}{2})$ avec $a$ un réel.

@emma12 , s'il faut utiliser le schéma que tu donnes, et si le point (?) peut être n'importe où sur la demi-droite en pointillés (centre du cercle trigonométrique compris) , tu peux préciser que les coordonnées de $P$ sont de la forme $(a\frac{\sqrt{2}}{2};a\frac{\sqrt{2}}{2})$ avec $\boxed{a\ge 0}$

Sans prendre le centre du cercle trigonométrique, la condition est $\boxed{a>0}$

A toi de savoir s'il faut prendre ou non ce centre.