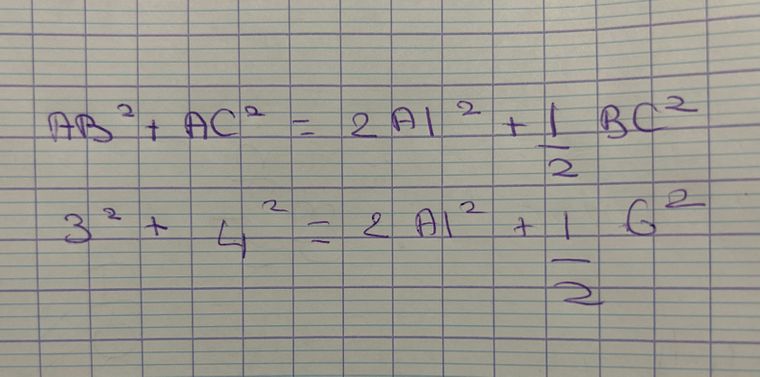Dm spé maths première
-
Hhiba_mrcnn dernière édition par
Bonjour pouvez vous m’aider pour cette question
Sachant que ABC un triangle. On note I le milieu de [BC].
- On suppose dans cette question que AB = 3, AC = 4 et BC = 6.
Calculer Al.
- On suppose dans cette question que AB = 3, AC = 4 et BC = 6.
-
mtschoon dernière édition par mtschoon

@hiba_mrcnn , bonsoir,
Dans ton cours, tu dois avoir un théorème dit "de la médiane" qui te permet de solutionner ton problème.
Eventuellement, regarde ici, page 8, paragraphe 1.4
(il y a la formule MA2+MB2=...MA^2+MB^2=...MA2+MB2=... et la démonstration.//www.vincentobaton.fr/MathsLycee/DocsPremiereS/2010_2011/Cours/CoursProduitScalairePartie02.pdf
Avec les notations de ton exercice, ce théorème te permet d'écrire :
AB2+AC2=2AI2+12BC2AB^2+AC^2=2AI^2+\dfrac{1}{2}BC^2AB2+AC2=2AI2+21BC2Tu remplaces AB,AC,BCAB,AC,BCAB,AC,BC par leurs valeurs et tu trouves 2AI22AI^22AI2 puis AI2AI^2AI2 puis AIAIAI
Tu peux donner ta réponse si tu souhaites une vérification.
-
Hhiba_mrcnn dernière édition par
Bonjour sa donne sa ?
-
@hiba_mrcnn Bonsoir,
C'est correct. Poursuis les calculs.
-
Hhiba_mrcnn dernière édition par
@Noemi
Je sais pas que vaut 2AI
-
Tu cherches AIAIAI, donc tu résous l'équation
32+42=2×AI2+12×623^2+4^2=2\times AI^2+\dfrac{1}{2}\times 6^232+42=2×AI2+21×62
9+16=.....9+16 = .....9+16=.....
-
Hhiba_mrcnn dernière édition par
-
Une erreur :
32+42=2×AI2+12×623^2+4^2=2\times AI^2+\dfrac{1}{2}\times 6^232+42=2×AI2+21×62
9+16=2×AI2+189+16 = 2\times AI^2+189+16=2×AI2+18
25−18=2AI225-18= 2AI^225−18=2AI2
2AI2=72AI^2=72AI2=7
....
-
Hhiba_mrcnn dernière édition par
Ce message a été supprimé !
-
Hhiba_mrcnn dernière édition par
7/2 = ? Puis le met en racine c sa ?
-
Hhiba_mrcnn dernière édition par
-
C'est correct.
AI2=72AI^2= \dfrac{7}{2}AI2=27, donne AI=±72AI = \pm \sqrt{\dfrac{7}{2}}AI=±27
Tu déduis AI=72AI = \sqrt{\dfrac{7}{2}}AI=27
-
BBlack-Jack dernière édition par
Alternative de résolution :
AlKashi dans le triangle ABC : AC² = AB² + BC² - 2.AB.BC.cos(ABC)
Toutes les longueurs sont connues et permettent de calculer : cos(ABC) = 29/36AlKashi dans le triangle AIB : AI² = AB² + BI² - 2.AB*BI.cos(ABC) où tout est connu ...
Et on trouve alors AI² = 7/2AI=72AI = \sqrt{\frac{7}{2}}AI=27