Logarithme népérien terminale

[hugo.mt_22]

Bonjour,
Je suis bloqué pour cette question. Serait-il possible d'avoir de l'aide?

Démontrer que pour tout réel x > 1, 1/x+1< ln(x+1)−ln(x) <1/x

On pourra étudier les variations d’une fonction u : x 7→ ln(x + 1) − ln(x) −1/x
et d’une fonction v : x 7→ln(x+1)−ln(x)−1/x+1

Merci d'avance

[Noemi]

@hugo-mt_22 Bonjour,

As-tu étudier les variations des fonctions indiquées ?

[hugo.mt_22]

@Noemi Non

[Noemi]

@hugo-mt_22

Donc fais l'étude, commence par calculer la dérivée.

Indique tes éléments de réponse si tu souhaites une vérification.

[hugo.mt_22]

@Noemi comment dériver cela?

[Noemi]

@hugo-mt_22

La dérivée de $ln(u(x))$ est $\frac{u^{\prime }(x)}{u(x)}$.

[mtschoon]

Bonjour,

@hugo-mt_22, je te développe un peu la fonction $U$ si besoin, pour $x>1$
$U^{\prime }(x)=\frac{1}{x+1}-\frac{1}{x}+\frac{1}{x^2}$
En réduisant au même dénominateur et en simplifiant le numérateur, tu dois trouver :
$U^{\prime }(x)=\frac{1}{x^2(x+1)}$
Donc $U^{\prime }(x)>0$ , $U$ strictement croissante.
Tu cherches la limite en $+\infty$

Tu dois trouver le tableau de variation:

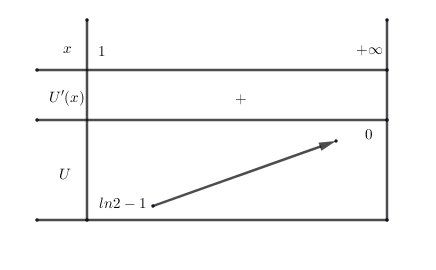
Conséquence : $U(x)<0$,c'est à dire
$ln(x+1)-lnx-\frac{1}{x}<0$, c'est à dire
$\boxed{ln(x+1)-lnx<\frac{1}{x}}$

Regarde tout ça de près et passe à l'étude de la fonction $V$
Tu dois trouver $V$ strictement décroissante de $ln2-\frac{1}{2}$ vers $0$, donc $V(x)>0$ ce qui te permet d'obtenir
$\boxed{ln(x+1)-lnx>\frac{1}{x+1}}$, d'où la réponse.

[mtschoon]

Bonjour,
Il était possible de faire autrement, à condition de connaître "aire et intégrale".

Pour $x>1$ , soit $f(x)=\frac{1}{x}$
$f$ strictement décroissante. Courbe en bleu foncé.

Points :
$A(x,0),B(x,\frac{1}{x}),C(x+1,0),D(x+1,\frac{1}{x})$ et
$E(x,\frac{1}{x+1},F(x+1,\frac{1}{x+1})$

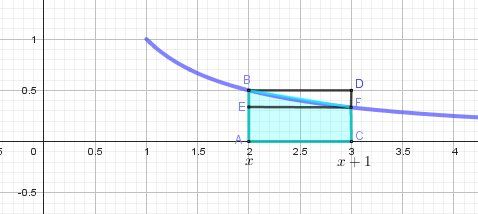
l'aire du quadrilatère curviligne $(ACFB)$ (zone bleu clair), en U.A. , est:
${\int }_x^{x+1}\frac{1}{t}dt=[lnt{]}_x^{x+1}=ln(x+1)-lnx$

Par encadrement :
$aire(ACFE)<aire(ACFB)<aire(ACDB)$
$1\times \frac{1}{x+1}<{\int }_x^{x+1}\frac{1}{x}dx<1\times \frac{1}{x}$

$\boxed{\frac{1}{x+1}<ln(x+1)-lnx<\frac{1}{x}}$