Determination du delta entre deux sinus

[Littledodger]

Bonjour à tous,

Je cherche à déterminer le delta t entre deux sinus alors que j'ai les informations suivantes :

• valeur max : 3.3 par exemple
• valeur min : 0 par exemple
• fréquence (50Hz)
• valeurs des deux sinus à un instant T et donc le delta entre les deux

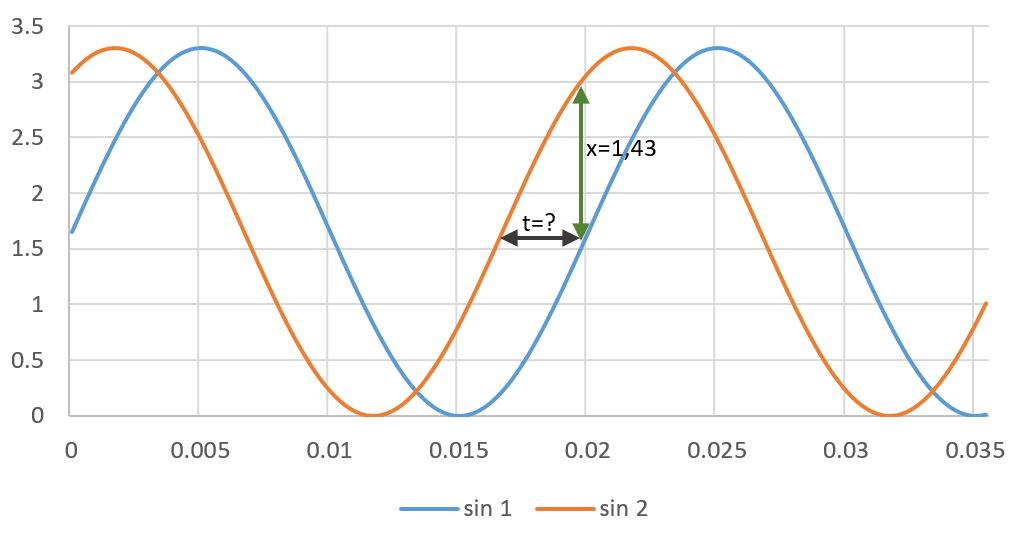
L'idée, c'est d'avoir une formule avec laquelle il serai possible de récupérer t alors que le delta entre les deux sinus ne sont pas forcément pris au niveau de la valeur moyenne...
Je ne sais pas si c'est possible pour tout dire ...

[Noemi]

@Littledodger Bonjour,

Un lien vers un site de physiques : https://zestedesavoir.com/tutoriels/2451/les-signaux-sinusoidaux-en-physique/dephasage-et-retard/

[Littledodger]

Bonjour @Noemi ,
Oui, je connais les relations Phi = Phi1-Phi2 et Delta t = Phi/2Pif mais le problème c'est que dans mon cas, Phi n'est pas connu...

[Noemi]

@Littledodger

Tu n'as pas les éléments pour déterminer les équations des courbes ?

[Littledodger]

J'ai des éléments mais pas assez pour en déterminer les équations, il manque Phi...

Sur l'exemple, la formule des deux courbes est :
en bleu : y(t) = 1.65 x sin (100 x Pi x t) + 1.65
en orange : y(t) = 1.65 x sin ((100 x Pi x t)+ Pi/3) + 1.65

Le problème, c'est qu'en pratique, je ne peux mesurer que le delta y entre les deux courbes à l'instant t.

[Noemi]

@Littledodger

A partir des équations indiquées, tu peux déduire le déphasage $\frac{\pi }{3}$.

[Littledodger]

@Noemi

Oui, je sais bien, c'est moi qui ai déterminé les formules et ajouté ce déphasage pour l'exemple, le problème, c'est que dans la pratique, je n'ai la formule d'aucune des deux courbes, seulement la pulsation, l'amplitude et le delta y à un instant t...

[Noemi]

@Littledodger

En physique, on détermine généralement $\Delta t$ directement à partir des signaux.

[Littledodger]

Sauf que je ne peux pas mesurer ce delta t, c'est justement, ce que je cherche à déterminer...

[Noemi]

@Littledodger

Avec les données, peux-tu écrire ?
$y_1=A_{1}sin(\omega t_1+\varphi )$ et
$y_2=A_{2}sin(\omega t_1)$

[Littledodger]

En partant de ta proposition, je suis arrivé à la formule suivante pour le Δt :

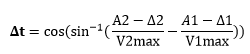
où A(1-2) Correspond à la valeur relevée à l'instant t
V(1-2)max correspond à la valeur max de chaque sinus moins l'offset éventuel
Δ(1-2) correspond à l'offset de chaque courbe

Je ne pense pas que ce soit plus factorisable...

[Littledodger]

Je suis en train de me demander si on a le droit de factoriser le sin-1 comme je l'ai fait !?
de sin-1(A) - sin-1(B) est-il égal à sin-1 (A-B) ?

[mtschoon]

@Littledodger , bonjour,

Comme je passe par là, je regarde seulement ta dernière question.
(je n'ai pas suivi ton topic)

Si $si{n}^{-1}$ est la fonction réciproque de $sin$ (c'est à dire notée habituellement $Arcsin$), c'est NON à ta question .

Tu peux seulement faire un test à la calculette pour t'en apercevoir :
$si{n}^{-1}(0,8)-si{n}^{-1}(0.1)\approx 0.827$ (angle en radians)
$si{n}^{-1}(0.8-0.1)\approx 0.775$ (angle en radians)

[Littledodger]

Oui, j'ai vu ça ^^
Merci pour ta réponse

[Noemi]

@Littledodger

Je ne trouve pas le même résultat.
j'arrive sauf erreur de calcul à :
$co{s}^2\varphi -\frac{2Y_1{Y}_2}{A_1{A}_2}cos\varphi +\frac{Y_1^2}{A_1^2}+\frac{Y_2^2}{A_2^2}-1=0$
Equation du second degré qui permet de déterminer $\varphi$.

[Littledodger]

@Noemi
Est-ce qu'il te serait possible de me donner ton cheminement pour arriver à cette équation s'il te plait ?

[Noemi]

@Littledodger

A partir de :
$Y_1=A_{1}sin(\omega t_1+\varphi )$ et
$Y_2=A_{2}sin(\omega t_1)$
et
$sin(\omega t_1+\varphi )=sin(\omega t_1)cos(\varphi )+cos(\omega t_1)sin(\varphi )$
soit en posant $cos(\omega t)$ et $sin(\varphi )$ positif
$\frac{Y_1}{A_1}=\frac{Y_2}{A_2}cos(\varphi )+\sqrt{1-\frac{Y_2^2}{A_2^2}}\times \sqrt{1-co{s}^2(\varphi )}$
puis
$\frac{Y_1}{A_1}-\frac{Y_2}{A_2}cos(\varphi )=\sqrt{1-\frac{Y_2^2}{A_2^2}}\times \sqrt{1-co{s}^2(\varphi )}$

Tu élèves au carré et tu simplifies l'expression