Calcule déciles, quartile et quintiles

Bonjour à tous,

J'espère que vous allez bien.

Je travaille actuellement sur un projet bénévole et j'ai besoin de déterminer les déciles d'un ensemble de données.
En fait j'ai le nombre de donnée, la plus petite donnée, la moyenne, la médiane, le quartile inférieur, le quartile supérieur, la plus haute donnée mais aussi la déviation standard mais j'ai besoin à partir de ces éléments de découper cet ensemble en quartile. Est-ce que c'est possible?

Voici les données dont je dispose:

Nombre de données (count): 90
Donnée la plus basse (low): 92.1
Quartile bas (lower quartile): 173.2
Moyenne : 281.9
Médiane: 252.8
Quartile supérieur (Uper quartile) : 345
Donnée la plus haute (high): 899.3
Déviation standard (standard deviation): 156

Merci beaucoup pour votre retour!

@Pierre444 , bonjour,

Tu indiques " j'ai besoin à partir de ces éléments de découper cet ensemble en quartiles"

Dans tes données, il y a tout ce qu'il faut :
Première quartile : 173.2
Médiane (deuxième quartile) : 252.8
Troisième quartile : 345

Donc , tu découpes en 4 intervalles :
De 92.1 jusquà 173.2
De 173.2 jusqu'à 252.8
De 252.8 jusqu'à 345
De 345 jusqu'à 899.3

Merci beaucoup pour ta réponse mtschoon! Il y a, en fait, une erreur dans ma question. Je voulais savoir si on pouvait découper cet ensemble de données de manière plus fine par exemple:

Diviser cet ensemble non plus en quartiles mais en quintiles et déciles? pour avoir un découpage plus fin à partir de ces mêmes données.
Etre capable de classer des données en terme de performance dans cet ensemble: par exemple si je récupère des données d'une association de pouvoir leur dire, vous faites partie des 9% les plus performants de votre catégorie (à partir de ces données partagées). Comment fait-on ce calcul et est-ce possible?
Merci pour votre retour,
Bien cordialement,

@Pierre444 Bonjour,

Pour un découpage précis et plus fin, l'ensemble des données est à mon avis indispensables. La connaissance de la plus basse donnée et du premier quartile nous donne aucune indication sur les termes entre les deux.

Merci beaucoup pour ta réponse Noémie. Donc on ne peut pas imaginer découper ces données de manière plus ou moins "logique" pour se donner une idée d'un découpage plus fin? Merci pour vos retours?

@Pierre444

Tu peux bien sur faire une proposition de décomposition "logique" mais cela donnera une possibilité parmi des milliers.
Par exemple prendre le milieu de chaque intervalle.

Bonjour,

@Pierre444 , comme te le dit Noemi, pour avoir un découpage plus fin, il faudrait connaître les données précises, et pas seulement les caratéristiques indiquées.

On peut penser à approcher la répartition par une répartition usuelle, uniforme ou normale, mais sur l'étendue des 90 données , ce n'est pas raisonnable...

La seule chose de juste est la répartition en 4 intervalles (avec les quartiles)

Pour illustration éventuelle, je te mets un lien :https://manuelnumeriquemax.belin.education/ses-premiere/topics/ses1-fm-315-a_lire-les-quantiles-quartiles-deciles-centiles

Sur chacun des 4 intervalles (liés aux quartiles), il n'y a vraiment aucune information...

On peut , sans aucune preuve, considérer que la répartition est uniforme sur chacun de ces intervalles...
Je vais te mettre quelques indications pour le cas où cette hypothèse te paraîtrait plausible.

Piste dans le cas d'une répartition uniforme sur [92.1 ; 173.2]

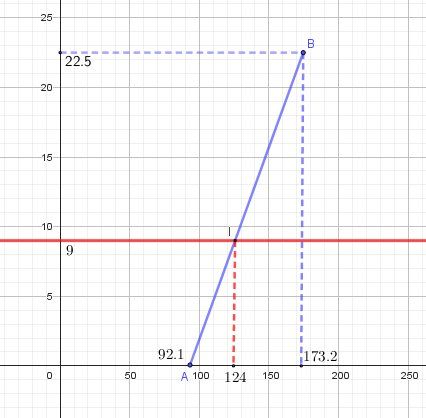
Dans ce repère :
en abscisse, il y a les données (de [92.1 ; 173.2] dans ce cas)
en ordonnée, il y a les effectifs cumulés .

$25$ % $(90) = 22.5$
Evdemment , ce n'est pas un nombre entier ! tu peux arrondir à $22$ ou $23$

Point $A$ de coordonnées $92.1)(0\ , \ 92.1)$
Point $B$ de coordonnées $22.5)(173.2\ ,\ 22.5)$

Fonction de répartition représentée par le segment $[A B]$ (en bleu sur le schéma) d'équation $y = a x + b$
En utilisant $A$ et $B$ , on obtient le système :
${0=92.1a+b22.5=173.2a+b\begin{cases}0=92.1a+b\cr 22.5=173.2a+b\end{cases}$

Après résolution, on trouve :
$a≈0.28a\approx 0.28$ et $b≈−25.55b\approx -25.55$ d'où :
$\approx 0.88x-25.55$

Pour obtenir la donnée $x$ correspondant à $10$ % de l'effectif total
$y = 10$ % $(90) = 9$ (droite en rouge sur le schéma)

Pour trouver $x$ , on résout :
$9≈0.88x−25.559\approx 0.88x-25.55$
Après résolution, on trouve : $x≈124x\approx 124$ (Point $I$ sur le schéma)

Conclusion : avec l'hypothèse de départ, on peut considérer qu'il y a, environ, $10$ % de l'effectif total pour lequel les données sont inférieures ou égales à 124.

Il est possible de raisonner de la même manière sur les trois autres lintervalles .

Bonjour mtschoon,
Merci infiniment pour ta réponse très complète. Ca m'aide vraiment beaucoup! La répartition uniforme pourrait faire l'affaire dans un premier temps. J'ai d'autres données qui portent sur un échantillon moins important que 90 données et donc l'écart-type est moins important (entre 15 et 30 selon les données. Est-ce que dans ce cas là une répartition uniforme serait plus proche de la réalité et donc plus facilement calculable?

Merci pour vos retour et encore merci mtschoon!

@Pierre444 , bonjour,

Contente d'avoir pu t'éclairer sur la démarche mais évidemment la répartition uniforme n'est qu'une hypothèse de travail.

Pour ta seconde série, difficile à dire ... Considérer que la répartition est uniforme est le plus simple.

Ce serait bien tout de même de pouvoir, si cela est possible, séparer la série en intervalles connus (comme ce qui a été proposé sur ton énoncé avec les quartiles ) et utiliser la répartition uniforme sur chaque intervalle (plus les intervalles connus sont petits, mieux c'est...).

Bon courage !