équation paramétrique à établir soit même
-
Livindiam Livin dernière édition par

Bonjour,
J'ai du mal avec les équations paramétriques qu'on doit "inventé" soit même: je doit déterminé l'équation paramétrique d'une droite qui est le point d'intersection de deux plans
J'ai posé x=t
Les équations cartésiennes des plans sont
P1 : 2x + y + 2z -4 = 0
P2 : 2x -4y =0J'ai résolu mon système et je tombe sur
x=t
y = -2t + 2,5
z = -10/8t +2 avec t appartient à RY'a t-il un moyen pour être sur que je ne me suis pas trompée ? Dans les questions suivantes cette équation pose un problème, ainsi je ne sais pas si elle est juste
Merci
-
@Livindiam-Livin Bonjour,
Vérifie tes calculs
4y=2x4y= 2x4y=2x donne y=x2y= \dfrac{x}{2}y=2x donc ....Pour une vérification, remplace les équations paramétriques dans les équations des plans.
-
Livindiam Livin dernière édition par

@Noemi Ok je vais vérifié tous mes calculs
-
Livindiam Livin dernière édition par

@Noemi Le plan est orthogonal à (CD) et passe par B(0,0,2)
J'ai donc déduit que le vecteur normal est le vecteur CD(2,-4,0)
J'ai trouvé 2x -4y = 0
-
mtschoon dernière édition par

Bonjour,
@Livindiam-Livin a dit dans équation paramétrique à établir soit même :
J'ai posé x=t
Les équations cartésiennes des plans sont
P1 : 2x + y + 2z -4 = 0
P2 : 2x -4y =0@Livindiam-Livin , avec ces données, ce que tu indiques pour yyy en fonction de ttt est bizarre.
Une réprésenration paramétrique de la droite d'intersection devrait être :
{x=ty=t2z=−54t+2\begin{cases}x=t\cr y=\dfrac{t}{2} \cr z=-\dfrac{5}{4}t+2\end{cases}⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧x=ty=2tz=−45t+2
-
Livindiam Livin dernière édition par

@mtschoon Re bonsoir,
L'équation cartésienne P1 est donné dans l'énoncé.
J'ai indiqué plus au d'après l'énoncé comment j'ai trouvé P2.Pensez vous qu'il y a une faute dans P2 ? Ou est ce mon équation paramétrique qui ne va pas et P2 est correcte ?
Je vais retenter le tout.
Merci
-
Si l'équation du plan est correcte, la réponse pour une représentation cartésienne a été donnée.
-
Livindiam Livin dernière édition par

@Noemi Je pensais que comme le plan passe par B, B appartient à celui ci.
Dans l'énoncé on ne m'indique pas un point qui appartient au plan. On me demande de trouver l'équation cartésienne P2 passant par B et orthogonal à (CD)
-
L'équation d'un plan est de la forme : ax+bx+cz+d=0ax+bx+cz+d=0ax+bx+cz+d=0
si le point BBB appartient au plan, il vérifie son équation, donc si tu as un doute vérifie l'équation du plan.
-
Livindiam Livin dernière édition par

@Noemi Lorsque je vérifie avec B(0,0,2) j'ai 2 x 0 - 4 x 0 + 0 x 0 +0 = 0 Car cz = 0 et d = 0
-
mtschoon dernière édition par

Bonjour,
@Livindiam-Livin , si tu as un doute, je pense que tu devrais écrire clairement la totalité de l'énoncé pour que l'on puisse vérifier si les deux équations de plans que tu as données au départ sont exactes.
-
Livindiam Livin dernière édition par

@mtschoon on a le point B(0,0,2) C(0,4,0) D(2,0,0)
le plan BCD : 2x+y+2z -4 = 0
On demande l'équation du plan p passant par B et orthogonal à( CD)
-
mtschoon dernière édition par mtschoon

@Livindiam-Livin , bonjour,
Tes équations de plans sont bien exactes
Plan (P1)(P_1)(P1) passant par B,C,DB,C,DB,C,D : 2x+y+2z−4=02x+y+2z-4=02x+y+2z−4=0
Plan passant (P2)(P_2)(P2) passant par BBB et orthogonal à(CD)(CD)(CD) : x−2y=0x-2y=0x−2y=0
-
Livindiam Livin dernière édition par

@mtschoon Merci !
-
mtschoon dernière édition par

De rien @Livindiam-Livin et bon travail !
-
Livindiam Livin dernière édition par Livindiam Livin

@mtschoon Bonsoir,
Avez vous une idée sur que peut représenter cette droite par rapport au triangle ABC du plan 1 ?
-
mtschoon dernière édition par mtschoon

@Livindiam-Livin , bonsoir,
Ce n'est pas génial, car ce n'est pas simple de faire une figure en 3D..., mais cela peut te donner une idée.
Le plan gris est le plan "horizontal" défini par les axes (Ox) et (Oy)
L'axe (Oz) est "vertical"
La droite (CD) est en noire
Le plan (P1)(P_1)(P1) est rose
Le plan (P2)(P_2)(P2) est bleu.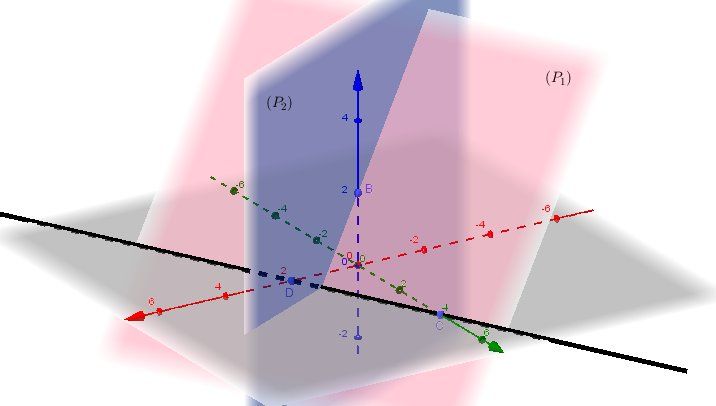
-
Livindiam Livin dernière édition par

@mtschoon Super, merci !
-
mtschoon dernière édition par

De rien @Livindiam-Livin , j'ai fait au mieux...