Calculer le Rayon d'un Arc

[longview]

Bonjour,
Les mathématiques s'invitent en lutherie.
Je ne savais pas quel partie du forum poster ce message.
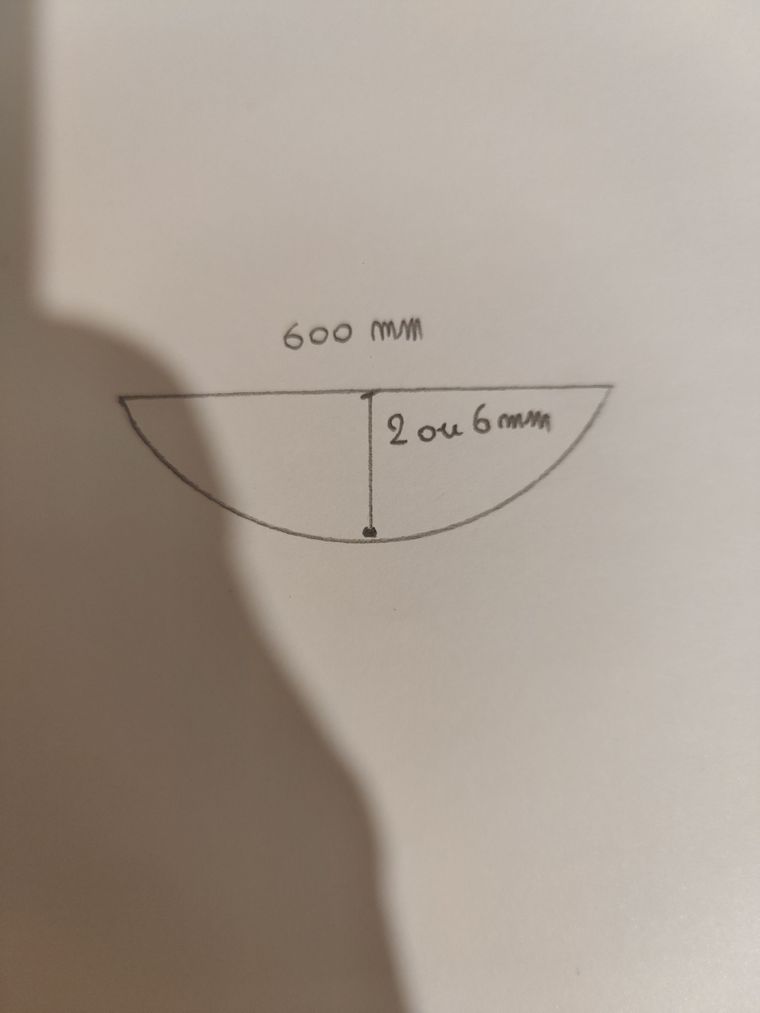
J'aurais besoin de connaitre le rayon d'un Arc je ne connais que la profondeur et la distance entre les deux côtés de l'arc.

Est ce que vous auriez la réponse pour pour une distance de 600mm et une profondeur de 6mm ainsi que pour une distance de 600mm et une profondeur de 2mm?

J'ai fait un petit dessin pour vous montrer.

Merci beaucoup de votre aide!

[Noemi]

@longview Bonjour,

Si tu peux déterminer le rayon $r$ et l'angle $\alpha$ qui délimite l'arc.
La longueur de l'arc est : $L=\alpha \times r$ si l'angle $\alpha$ est en radian ou
$L=\frac{\alpha \times \pi \times r}{180}$ si l'angle $\alpha$ est en degré.

La mesure de la corde est $C=2\times r\times sin(\frac{\alpha }{2})$

[longview]

@Noemi Bonjour Noemi,
Merci. J'avoue que tu m'as complètement perdue avec ta réponse.

Je n'ai aucune autre mesure que celles que j'ai donné.

[Noemi]

@longview

Peux-tu faire un schéma et déterminer le centre du cercle ?

[mtschoon]

Bonjour,

Pour un schéma , en voilà un (sans tenir compte des mesures)

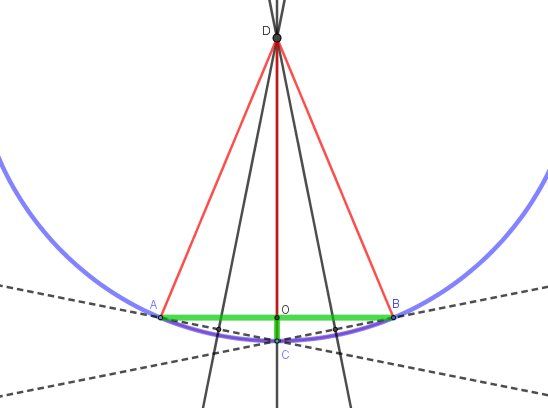
Si j'ai bien lu, @longview , tu connais La mesure de $[AB]$ (600 mm) et , en appelant $O$ le milieu de [AB], tu connais la mesure de $[OC]$ (2 ou 6 mmmm) (en vert sur le schéma).

Soit $D$ le centre du cercle bleu passant par $A,C,B$

@longview , quand tu parles de "rayon d'un arc" , est-ce que tu parles du rayon $R=DA=DB=DC$ (en rouge sur mon schéma) ?

Merci d'indiquer si c'est bien cela que tu cherches (ou autre chose), car ce serait dommage de te proposer des calculs inutiles.

Ce serait bien aussi que tu indiques ton niveau, car "Autres classes", c'est vague...

[Noemi]

@longview

Détermine une relation entre l'angle $\widehat{OCB}$ et l'angle $\widehat{CDB}$.
Puis exprime la mesure de $DB$ en fonction des mesures de $OB$ et $OC$.

[mtschoon]

Bonjour,

@longview , si c'est bien le rayon $R$ que je t'ai indiqué que tu cherches, tu peux utiliser la suggestion de Noemi.

Tu peux aussi faire un calcul de géométrie analytique pour le trouver, si tu le souhaites.

Tu as le choix !

Je te donnes, si besoin, des pistes pour l'analytique.
Tu te places dans le repère orthonormé d'origine $O$ , usuel.
(Ne tiens pas compte des graduations des axes du schéma joint, car elles ne correspondent pas à tes mesures...le schéma est seulement là pour comprendre la démarche)

$A$ a pour coordonnées $(-300,0)$ et $B$ a pour coordonnées $(+300,0)$ pour avoir $AB=600$ (en mm)

Pour avoir $OC=2$ ( en mm) , tu prends $C$ pour coordonnées $(0,-2)$

$D$ est à l'intersection de la médiatrice $(\Delta )$ de $[AC]$ avec l'axe des ordonnées et avec la médiatrice $({\Delta }^{\prime })$ de $[BC]$

Par exemple, tu peux trouver une équation de $(\Delta )$ en écrivant que pour tout $M$de coordonnées $(x,y)$ de $(\Delta )$ : $MA=MC$
L'axe des ordonnées a pour équation $x=0$
Tu obtiendras ainsi l'ordonnée $y_D$ du point $D$, égale à $OD$
Au final, $R=OD+OC$

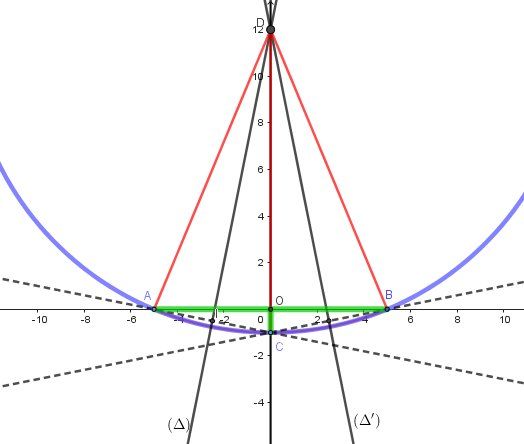
Bons calculs.
Tu peux donner tes calculs/réponses, si tu souhaites une vérification.

[longview]

Bonjour,
Merci beaucoup pour vos réponses.
Je vais prendre le temps de regarder ça la semaine prochaine.

Mtschoon, c'est bien ça. J'ai les mesures AB et OC et je cherche le Rayon R.

Au sujet de mon niveau, je devait être passable en terminale et je n'ai plus fait de maths depuis plus de 10 ans. Passable est peut être même trop gentil!

Pour vous expliquer ma démarche, je me suis mise à la lutherie, je vais commencer ma deuxième guitare et j'ai besoin d'acheter ce qu'on appelle une "radius dish". Une planche qui est creusée à un certain radius ou rayon.
Le luthier que je connais n'a pu me donner que ces mesures. Il ne connait pas le rayon exacte et je ne trouve rien dans les livres.
Les rayons vont souvent de 12 pieds à 40 pieds (il faudra que je reconvertisse mon résultat en pied), les possibilités sont donc un peu vastes.

[mtschoon]

@longview , bonjour,

Merci pour ces précisions.

C'est donc bien le $R$ proposé que tu cherches.
C'est un problème "très concret" que tu as à résoudre.

Bons calculs !
Tu auras des indications plus complètes si tu n'y arrives pas .

[mtschoon]

Bonjour,

@longview , une réflexion...

Es-tu vraiment sûr des mesures indiquées ?

Je viens de faire les calculs , en prenant 600mm de "largeur" de l'arc et 2mm en "profondeur".

Vu la petitesse de la "profondeur" (presque négligeable) par rapport à la très grande "largeur", le rayon $R$ est énorme ! ! !.

Je n'y connais rien en lutherie, mais j'ai un doute.
Ce serait bien que tu vérifies tes données.

12 pieds=3657.6 mm
40 pieds=12192 mm
Avec seulement 2mm de profondeur et 600 mm de largeur, le rayon $R$ n'est pas dans cet ordre de grandeur...( ça fait environ $73.82pieds)$

Par contre, en prenant toujours 600mm de "largeur" de l'arc et 6mm en "profondeur", on trouve un rayon $R$ dans la fourchette indiquée.
Sauf erreur, avec 6 mm de largeur $R=7503mm$
En pieds , cela fait environ $26.61pieds$

Avec une profondeur de 4 mm , ça va encore.
en prenant toujours 600mm de "largeur" de l'arc et 4mm en "profondeur", on trouve un rayon $R$ de $11252mm$ c'est à dire environ $36.91pieds$.

En bref , ce 2 mm de profondeur semble vraiment trop petit. (si l'on garde 600 mm de largeur)
Même avec 3 mm de profondeur , ça ne va pas...

Au final, en gardant 600 mm de largeur, $R$ est dans la fourchette que tu donnes en prenant une profondeur comprise entre 4 mm et 12 mm.

Evidemment, tu peux changer la largeur !

[Larry Novack]

Bonjour, je viens de m'inscrire à ce groupe mais je pense que c'est exactement ce que je cherchais. Je fais de petites présentations de mathématiques sur mesure et j'ai un peu de mal à trouver des images de bonne qualité en ce moment. J'espère que ce groupe pourra me dire où je peux trouver des images de bonne qualité.

[mtschoon]

@Larry-Novack , je crois que tu t'es un peu trompé de topic car ta question n'a rien à voir avec le sujet de ce topic...relatif au rayon d'un arc de cercle...

Tu auras dû ouvrir ta propre discussion, et dans une rubrique plus adaptée, peut-être Maths-Outils...

Personellement, je fais des constructions géométriques avec Geogebra (logiciel gratuit)

[longview]

@mtschoon
Désolée pour le temps de réponse.
Mtschoon, je crois que tu touches un très bon point. Ou du moins, les mesures du luthier sont justes, je l'ai recontacté. Mais il utilise sans doutes un rayon bien différent des standards. (Ça complique ma tâche de savoir ce que je veux/dois exactement acheter)

Je n'ai pas réussi à faire ton calcul... Ton dernier m'a par contre donné un bon ordre de grandeur.

Est-ce que tu aurais la gentillesse de me développer un des calculs avec (une valeur) par exemple 6mm de profondeur? (Remplacer ton calcul par des valeurs concrètes)

J'essaierai de le refaire avec d'autres valeurs et ça me permettra de comprendre comment tu as fait.
Et comme ça j'aurais appris quelque chose.

En tout cas, merci beaucoup pour ton aide. Ton dernier message m'a beaucoup aidée.

[mtschoon]

@longview , bonsoir,

Effectivement, ça fait tout juste 2 mois que tu as posé ta question et que je t'ai répondu...

J'avoue que je ne sais même plus très bien de quoi il s'agit.

Lorsque j'aurais le temps de m'y remettre, je te donnerais un calcul détaillé.

Bonne soirée.

[mtschoon]

@longview , bonjour,

Comme tu le souhaites (d'après ta dernière question), je t'indique les calculs du rayon $R$ avec 600 mm de largeur et 6 mm de profondeur.

On travaille dans le repère (et les notations) de mon dernier schéma.
Comme déjà indiqué, les graduations des axes du schéma ne correspondent pas aux mesures réelles , bien sûr.

1 ) $A$ a pour coordonnées $(-300,0)$, $C$ a pour coordonnées $(0,-6)$
Soit $M(x,y)$ un point quelconque de $(\Delta )$ médiatrice de $[AC]$
$MA=MC$
Pour éviter les radicaux, on élève au carré , et l'on peut écrire $A{M}^2=C{M}^2$
$(x+300{)}^2+(y-0{)}^2=(x-0{)}^2+(y+6{)}^2$
En développant,
$x^2+90000+600x+y^2=x^2+y^2+36+12y$
En simplifiant,
$90000+600x=36+12y$
$7500+50x=3+y$
$\boxed{50x-y+7497=0}$ : Equation de $(\Delta )$

[mtschoon]

2 ) $B$ a pour coordonnées $(300,0)$, $C$ a pour coordonnées $(0,-6)$
Soit $M(x,y)$un point quelconque de $({\Delta }^{\prime })$ médiatrice de $[BC]$
$MB=MC$
Pour éviter les radicaux, on élève au carré , et l'on peut écrire $B{M}^2=C{M}^2$
$(x-300{)}^2+(y-0{)}^2=(x-0{)}^2+(y+6{)}^2$
En développant,
$x^2+90000-600x+y^2=x^2+y^2+36+12y$
En simplifiant,
$90000-600x=36+12y$
$7500-50x=3+y$
$\boxed{-50x-y+7497=0}$ : Equation de $({\Delta }^{\prime })$

[mtschoon]

3 ) On analyse le système composé des deux équations des médiatrices trouvées, pour obtenir l'ordonnée de leur point d'intersection $D$

$\{\begin{array}{l}50x-y+7497=0\\ -50x-y+7497=0\end{array}$

En ajoutant membre à membre :
$-2y+2(7497)=0$
En simplifiant par $2$
$-y+7497=0$
$y=7497$
L'ordonnée du point $D$ est $7497$

Conclusion :

$OD=7497mm$

$R=OD+OC=(7497+6)mm=7503mm$

On peut utiliser un convertisseur en ligne pour obtenir la mesure en pieds.

$\boxed{R\approx 26,61pieds}$

Bonne lecture !