Fonction et e népérien

[Amina Bayana]

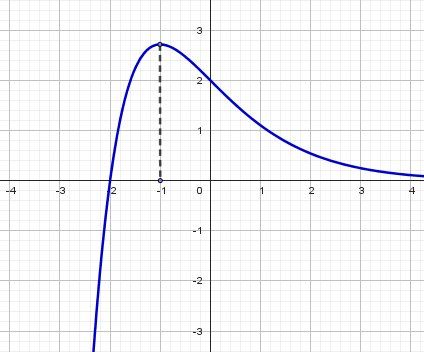
Bonsoir à tous svp j'ai une petite difficulté. J'ai du mal à trouver les limites aux bornes de + et - l'infinie ainsi que la dérivée de cette fonction :f(x)=(x+2)exp^-x

[Noemi]

@Amina-Bayana Bonsoir,

Pour la limite en $+\infty$, mets $x$ en facteur.
Pour la dérivée, utilise la dérive de $U\times V$.

Indique tes calculs si tu souhaites une vérification.

[Amina Bayana]

@Noemi oui merci j'ai appliqué la formule pour f=u×v f'=u'v+uv' ça m'a donné comme dérivée (x-1)e^-x

[Noemi]

@Amina-Bayana

c'est faux :
$u(x)=x+2$ donne $u^{\prime }(x)=1$ et
$v(x)=e^{-x}$ donne $v^{\prime }(x)=-e^{-x}$

Vérifie tes calculs.

[mtschoon]

Bonjour,

@Amina-Bayana , j'espère que tu as refais le calcul de $f^{\prime }(x)$avec les réponses de Noemi.

Tu dois trouver $f^{\prime }(x)=(-x-1)e^{-x}$

Remarque :
Avec cette dérivée, vu que pour tout $x$ réel, $e^{-x}>0$, tu peux déduire que $f^{\prime }(x)$ est du signe de $(-x-1)$ donc sens de variation de $f$ facile à trouver.

Bon calcul.

[mtschoon]

@Amina-Bayana , quelques indications complémentaires sur les limites.

Lorsque $x$ tend vers $+\infty$, pour te ramener à des formules usuelles de ton cours, tu transformes $f(x)$

$f(x)=\frac{x+2}{e^x}=\frac{x}{e^x}+\frac{2}{e^x}$

$f(x)=\frac{1}{\left(\frac{e^x}{x}\right)}+\frac{2}{e^x}$

Regarde les propriétés vues en cours.

Au final, tu dois trouver

$\boxed{\underset{x\to +\infty }{\lim }f(x)=0}$

Lorsque $x$ tend vers $-\infty$, c'est assez immédiat avec directement l'expression de l'énoncé :
$f(x)=(x+2)e^{-x}$

$(x+2)$ tend vers $-\infty$
Lorsque $x$ tend vers $-\infty$, $-x$ tend vers $+\infty$ , donc $e^{-x}$ tend vers $+\infty$ (voir cours)

Tu cherche la limite du produit (voir cours)

Au final, tu dois trouver

$\boxed{\underset{x\to -\infty }{\lim }f(x)=-\infty }$

Bons calculs.

[mtschoon]

@Amina-Bayana

Représentation graphique de $f$