Etude d'une fonction avec exponentielle.

[hiba_mrcnn]

Devoir spé maths première
Bonjour quelqu’un peut t’il m’aider à résoudre ce tte exo :

Soit la fonction g, définie sur tous les réels par g(x) = 1-x + ex
) Déterminer les variations de g.
2) Determiner I extremum local de g puis en déduire le signe de g(x).
3) On définit maintenant la fonction f sur IR par f(x) = x +1+ X.
Démontrer que pour tout réel x on a : f(x) = e-*g(x).
4) En déduire de la question 3) les variations de f.
5) Donner l'équation de la tangente à C (courbe représentative de f dans un repère orthonormé) au point d'abscisse 0
On note i la droite représentant cette tangente dans le repère.
6) Etudier la position relative de C et de T.

[Noemi]

@hiba_mrcnn Bonjour,

La fonction est-elle : $g(x)=1-x+e^x$ ?

Indique tes éléments de réponses et la question qui te pose problème.
Pour les variations, étudie le signe de la dérivée :
$g^{\prime }(x)=-1+e^x$

[hiba_mrcnn]

@Noemi
Oui je n’ai pas trouver

[Noemi]

@hiba_mrcnn

Commence par résoudre l'équation $e^x=1$.

[mtschoon]

Bonjour,

Bizarre cette question en Première...
La fonction exponentielle se traite en principe en Terminale....

@hiba_mrcnn , je te conseille de revoir ton cours sur la fonction exponentielle .

$e^x=1$ <=> $x=0$

Quelques pistes pour les variations de $g$

$g^{\prime }(x)=-1+e^x$
(Noemi a écrit $f^{\prime }(x)$ à la place de $g^{\prime }(x)$, par erreur.)

$g^{\prime }(x)=0$ <=>$-1+e^x=0$ <=> $e^x=1$ <=> $x=0$
$g^{\prime }(x)<0$ <=>$-1+e^x<0$ <=> $e^x<1$ <=> $x<0$
$g^{\prime }(x)>0$ <=>$-1+e^x>0$ <=> $e^x>1$ <=> $x>0$

Je t'indique le tableau de varations de g que tu dois trouver .
Les limites en $-\infty$ et $+\infty$ ne sont pas indispensables , vu le but de la question.

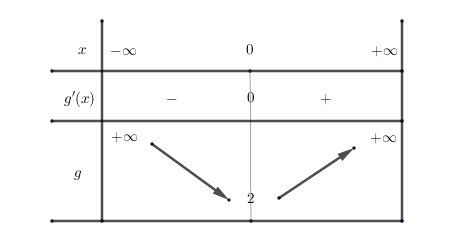
Vu que le minimum de $g(x)$est strictement positif ($2$), tu peux déduire que pour tout $x$ réel, $g(x)$ est strictement positif.

Regarde cela de près.

Pour la 3), tu as écrit f(x)=x+1+X et f(x) = e-*g(x).
Si tu as besoin d'aide , tu devrais revoir ces écritures ....confuses...