Vecteurs et coordonnées de droites

Salut,
J'ai beaucoup de mal à faire cette exo, est-ce que vous pouvez m'aider?

Voici l'énoncé:
Dans le plan muni d'un repère orthonormé, on considère les droites d1 d'équation x + 5y + 9 = 0, d2 d'équation 7x - 3y = 13 et d3 d'équation 6x -4y =9. Les droites d1 et d2 se coupent à une équation de la droite passant par P et perpendiculaire à d3?

A) 2x + 3y + 4 = 0
B) y + 3/2 = -3/2x +1
C) x = -3/2y +2
D)3x + 2y +1 = 0

Merci beaucoup!

Bonjour,

Bizarre,

safia adili = Sasha-BOOKSSS ?

Pourquoi avoir deux inscriptions et deux pseudos ?

Bonjour,

@mtschoon a dit dans Vecteurs et coordonnées de droites :

Bonjour,

Bizarre,

safia adili = Sasha-BOOKSSS ?

Pourquoi avoir deux inscriptions et deux pseudos ?

Merci pour une explication de ce qui semble être une double inscription.

Pistes,

Schéma :

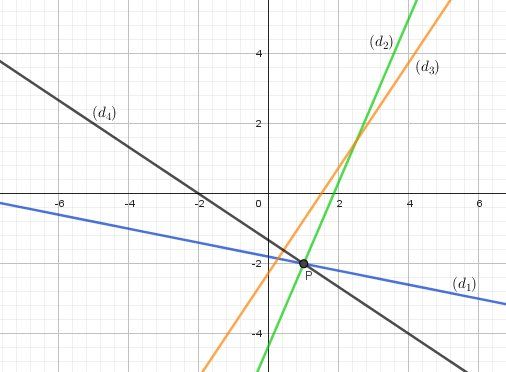
$d_4)$ est la droite cherchée.
Son équation est $2 x + 3 y + 4 = 0$

La réponse est $A)$

Pistes de calculs,

Pour trouver les coordonnées de $P$ , tu résous le système :
${x+5y+9=07x−3y=13\begin{cases} x+5y+9=0\cr 7x-3y=13\end{cases}$

Tu dois trouver $x = 1$ et $y = - 2$
Donc $P$ a pour coordonnées $(1, - 2)$

Ensuite, tu cherches l'équation de la droite $d_4)$ passant par $P$ est perpendiculaire à $d_3)$

Une méthode en passant par les coefficients directeurs de droites à été indiquées ici :
https://forum.mathforu.com/topic/33863/les-vecteurs-directeurs
Tu peux l'utiliser.

Tu peux aussi passent par les vecteurs directeurs (tu dois connaître vu que tu postes en Terminale)
Un vecteur directeur de $d_3)$ , donné par l'équation, a pour coordonnées $(4, 6)$

Tu peux prendre un vecteur directeur avec des coordonnées plus simples $U→(2,3)\overrightarrow{U}(2,3)$

Soit $V→(a,b)\overrightarrow{V} (a,b)$ un vecteur directeur de $d_4)$
$U→.V→=0\overrightarrow{U}.\overrightarrow{V}=0$
$2 a + 3 b = 0$
Tu peux prendre $a = - 3$ et $b = 2$ donc $V→(−3,2)\overrightarrow{V} (-3,2)$
Tu en déduis qu'une équation de $d_4)$ peut s'écrire :
$2 x + 3 y = c$

En remplaçant $x$ et $y$ par les coordonnées de $P$ , tu obtiendras $c = - 4$ d'où une équation de $d_4)$ : $2x+3y=−4\boxed{2x+3y=-4}$

Bons calculs.

@mtschoon Désolé, mon ordinateur ne fonctionne plus j'ai donc perdu mes identifiants

mercii pour la solution je comprends mieux

Merci pour l'information: problème informatique...

Bon travail !