Trouver les coordonnées d'un point

Bonjour , j'aurais besoin d'aide pour trouver les coordonnées du point de sachant que d est le 4eme sommet du parallélogramme ABCD et que nous connaissons déjà:
A(6;3) B(11;10) C(25;0)

@zoeeee Bonjour,

Calcule les coordonnées du vecteur $AB→\overrightarrow{AB}$
puis exprime les coordonnées du vecteur $DC→\overrightarrow{DC}$ en fonction des coordonnées du point $D (x; y)$
puis tu résous $AB→=DC→\overrightarrow{AB}=\overrightarrow{DC}$ .

Merci Black-Jack c'est une erreur en écrivant.

indique tes calculs et/ou résultats si tu souhaites une vérification.

@Noemi merciii beaucoup !!

@zoeeee

Tu as trouvé les coordonnées du point $D$ ?

@Noemi oui D( 20; -1)

@zoeeee

Vérifie tes calculs pour l'ordonnée en utilisant la relation $AB→=DC→\overrightarrow{AB}=\overrightarrow{DC}$ .
J'ai rectifié mon erreur dans le précédent message.

@Noemi a dit dans Trouver les coordonnées d'un point :

@zoeeee Bonjour,

Calcule les coordonnées du vecteur $AB→\overrightarrow{AB}$
puis exprime les coordonnées du vecteur $CD→\overrightarrow{CD}$ en fonction des coordonnées du point $D (x; y)$
puis tu résous $AB→=CD→\overrightarrow{AB}=\overrightarrow{CD}$ .

indique tes calculs et/ou résultats si tu souhaites une vérification.

Bonjour,

Si on respecte les "habitudes actuelles", on trouve les sommets dans l'ordre en "tournant" autour de la figure. (sens antihorlogique pour figure directe et sens horlogique pour figure indirecte

On a alors ceci :

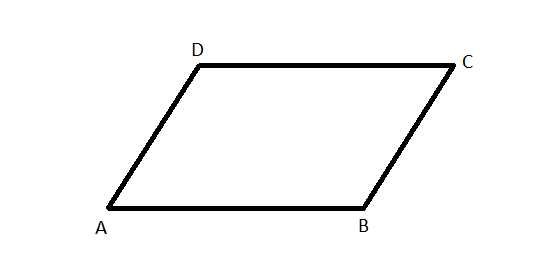
Sans titre.png

Si on respecte cela, alors il faut : $AB→=DC→\overrightarrow{AB} = \overrightarrow{DC}$

On trouve évidemment d'autres conventions pour repérer les sommets ... mais c'est de plus en plus rare.

@Black-Jack Bonjour,

Merci pour cette intervention, c'est une erreur d'écriture.
Ce type d'erreur, je ne suis pas la seule à en faire, je ne me permets pas pour l'instant de rectifier les réponses d'un contributeur autre que celui, (celle), qui a posé l'exercice.