Position relative de deux droites dans l'espace

Bonjour,
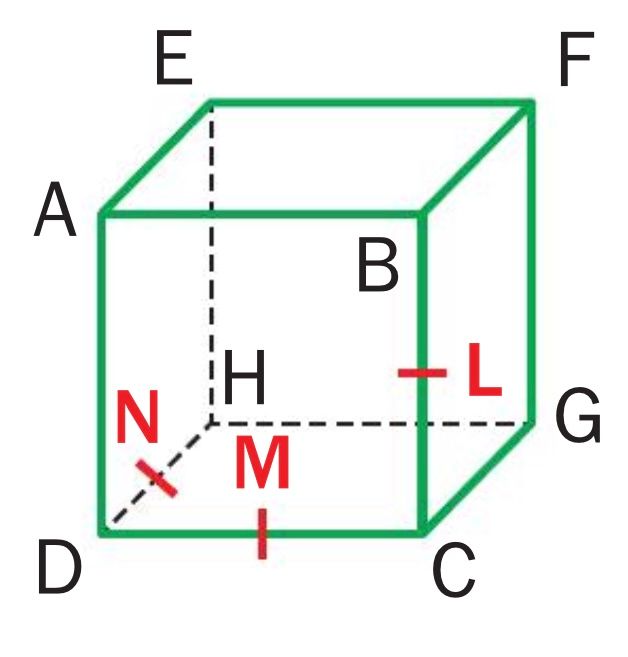
ABCDEFGH est un cube. L,M et N sont les milieux des segments [BC] [DC] et [DH]. Détemriner, en justifiant, les positions relatives des droites et plans suivants.

J'ai réussi à montrer (ML) et (HF) sont parallèles avec la relation de Chasles :
ML = MC + CL
<=> ML = 1/2DC+1/2CB
<=> ML = 1/2DB
<=> ML = 1/2 HF
D'où ML et HF sont colinéaires. Donc (ML)//(HF) et (ML) et (HF) coplanaires.

J'ai aussi réussi à montrer qye (HM) et (CG) sont complanaires sécantes :
(HM) C (DCG) et (CG) C (DCG).
Donc (HM) et (CG) sont complanaires.
(HM) et (DH) sont sécantes en H et (CG) // (DH). Or si deux droites sont parallèles, alors tout droite sécante à l'une est sécante à l'autre. Donc (HM) et (CG) sont sécantes.

Mais je bloque pour (AD) et (GM). Merci pour votre aide![text alternatif]

"complanaires" est une erreur de frappe. Je voulais dire "coplanaires".

Bonjour,

Une méthode parmi d'autres ...

Les droites (GM) et (AD) ne sont pas concourantes (car (MG) ne passe pas par D et donc ...)

Dans le repère(D , vect(DC), vect(DH) , vect(DA)), on a :

D(0;0;0)
A(0;0;1)
G(1;1;0)
M(1/2;0;0)

vect(AD) = (0 ; 0 ; -1)
vect(GM) = (-1/2 ; -1 ; 0)
vect(GM) . vect(AD) = 0 * (-1/2) + (0 * -1) + (-1 * 0) = 0

Et donc (GM) et (AD) sont orthogonales.

Merci. Mais, malheureusement, je n'ai pas encore vu les coordonnées dans l'espace.

@Suunh Bonjour,

Commence par montrer que ces deux droites ne sont pas coplanaires.

(AD) et (GM) ne sont pas dans le même plan. (AD) appartient à (ADH) alors que (GM) appartient à (GMC). Donc non (AD) et (GM) non coplanaires

@Suunh

Il reste à vérifier si les droites sont parallèles ou perpendiculaires.

Bonjour,

Ne pas confondre "perpendiculaires" et "orthogonales"

Après avoir montré que (AD) et (DG) n'étaient pas coplanaires ... (1)

Deux droites sont orthogonales lorsque les parallèles à ces deux droites, menées par un point quelconque de l'espace, sont perpendiculaires. (2)

Trace la parallèle à (MG) passant par D. Cette droite est dans le plan DCGH et est perpendiculaire à (AD) car ...

(1) et (2) --> (MG) et (AD) sont orthogonales.

On n'a pas encore vu cette notion de perpendiculaire / orthogonale. On a juste vu que deux droites peuvent être soit coplanaires (parallèles strictes, confondus, sécantes) ou non-coplanaires

@Suunh a dit dans Position relative de deux droites dans l'espace :

On n'a pas encore vu cette notion de perpendiculaire / orthogonale. On a juste vu que deux droites peuvent être soit coplanaires (parallèles strictes, confondus, sécantes) ou non-coplanaires

Bonjour,

En TERMINALE S ?

Je ne connais pas les programmes actuels, mais c'est quand même interpellant.

Je ne dis pas que je ne sais pas ce que sont deux droites orthogonales. Simplement que cela ne figure pas dans mon cours, donc j'imagine qu'il ne faut pas l'utiliser

@Suunh a dit dans Position relative de deux droites dans l'espace :

Je ne dis pas que je ne sais pas ce que sont deux droites orthogonales. Simplement que cela ne figure pas dans mon cours, donc j'imagine qu'il ne faut pas l'utiliser

Bonjour,

J'ose espérer que si la notion de perpendiculaire est connue (probablement depuis la 5 éme ?, avec l'étude des triangles rectangles ), on est censé pouvoir l'utiliser arrivé en Terminale.

Mais plus rien ne m'étonne.
Fais comme tu le sens.