dm maths sur les suites

bonjour j’ai besoin d’aide pour un dm de maths sur les suites, je ne comprends vraiment pas du tout

Pour tout n entier naturel, on note un l'aire du domaine délimité par l'axe des abscisses et les deux demi-cercles consécutifs ayant pour diamètres n + 2 et n + 1.

Quelle est la nature de la suite (Un)nEN?
Calculer la somme Uo + U1 + U2 + ... + u7.

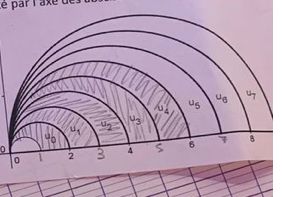
@srxxh Bonsoir,

As tu calculé $u_0$ ? $u_1$ ? ....
$u0=12(π×12−π×(12)2)=...u_0= \dfrac{1}{2}(\pi\times 1^2-\pi\times(\dfrac{1}{2})^2)= ...$

@Noemi j’ai essayé mais sans trouvé la formule à utiliser
donc c’est une suite géométrique ? de raison 0,5pi ?

@srxxh

Non, tu soustrais l'aire de deux demi-disques.
L'aire d'un disque est $π×R2\pi\times R^2$ .

Fais les calculs :
$u0=12(π×12−π×(12)2)=38πu_0= \dfrac{1}{2}(\pi\times 1^2-\pi\times(\dfrac{1}{2})^2)= \dfrac{3}{8}\pi$

$u1=12(π×(32)2−π×(1)2)=....u_1= \dfrac{1}{2}(\pi\times (\dfrac{3}{2})^2-\pi \times(1)^2)= ....$

@Noemi donc u1 = 5/8pi, u2 = 7/8pi, u3 = 9/8pi et ainsi de suite, donc une suite arithmétique de raison 2/8 ?

@srxxh

Oui suite arithmétique de raison $2π8=π4\dfrac{2\pi}{8}=\dfrac{\pi}{4}$ .

Calcule la somme en utilisant la relation pour la somme des termes d'une suite arithmétique.

@Noemi la somme c’est 8x(3/8pi+17/8pi) le tout/2 = 10pi ?

@srxxh

C'est juste.

@Noemi parfait merci beaucoup ça m’a aidé à comprendre !!

@srxxh

C'est très bien, tu as su suivre les conseils et terminer l'exercice.

Bonjour,

En voila encore un qui supprime son message lorsque l'aide a été donnée.

Ce genre de comportement devrait aboutir à une exclusion.

@Black-Jack a dit dans dm maths sur les suites :

Bonjour,

En voila encore un qui supprime son message lorsque l'aide a été donnée.

Ce genre de comportement devrait aboutir à une exclusion.

Message revenu ...
Par l'auteur initial ou par la modération, je ne sais pas.

@Black-Jack Bonjour,

C'est la modération qui a rendu visible l'énoncé. Un message a été transmis à srxxh.

@Noemi a dit dans dm maths sur les suites :

@Black-Jack Bonjour,

C'est la modération qui a rendu visible l'énoncé. Un message a été transmis à srxxh.

Merci.