Question exercice géométrie dans l’espace

[hiba_mrcnn]

Bonjour quelqu’un peut m’aider pour c’est deux dernière question énoncé :

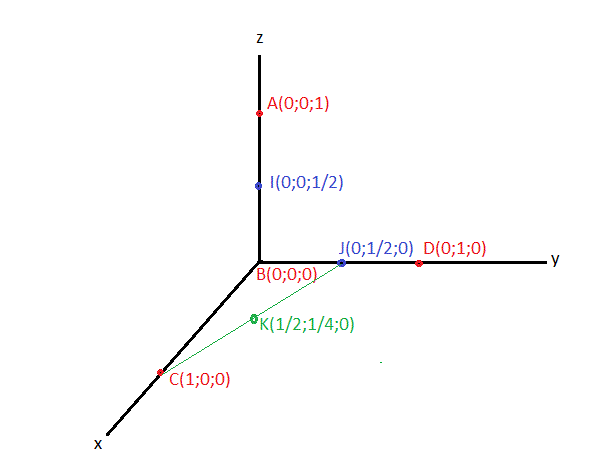
On considère un tétraèdre ABCD, les point I, J et K milieux respectif des segments [AB], [BD] et [CJ] et les points G et H définis par {AG}=2/3{AJ} et {BH}=2/3{BC} :

b)Déterminer leur position relative.

c)Que peut-on en déduire?

[Noemi]

@hiba_mrcnn Bonsoir,

Les positions relatives de quels points ?
Tu devrais écrire l'énoncé en entier et indiquer tes éléments de réponse.

[hiba_mrcnn]

@Noemi

1)Determiner les coordonnées des points de la figures dans le repère (B;{BC};{BD};{BA})

2)a)Montrer qu'il existe des reels a et b tels que {IK}=a {IG}+b{IH}

b)Que peut-on déduire pour les points G, H, I et K ?

3)a)Déterminer les représentations paramétriques des droites (IG) et (HK).

b)Déterminer leur position relative.

c)Que peut-on en déduire?

[Black-Jack]

@hiba_mrcnn a dit dans Question exercice géométrie dans l’espace :

@Noemi

1)Determiner les coordonnées des points de la figures dans le repère (B;{BC};{BD};{BA})

2)a)Montrer qu'il existe des reels a et b tels que {IK}=a {IG}+b{IH}

b)Que peut-on déduire pour les points G, H, I et K ?

3)a)Déterminer les représentations paramétriques des droites (IG) et (HK).

b)Déterminer leur position relative.

c)Que peut-on en déduire?

Bonjour,

Voir dessin (et comprendre)

2a)

$\overrightarrow{AJ}=(0;1/2;-1)$

$\frac{2}{3}\overrightarrow{AJ}=(0;1/3;-2/3)$

$\overrightarrow{AG}=(0;1/3;-2/3)$

$X_G-X_A=0$ --> $X_G-0=0$ ---> $X_G=0$
$Y_G-Y_A=1/3$ --> $Y_G-0=1/3$ ---> $Y_G=1/3$
$Z_G-Z_A=-2/3$ --> $X_G-1=2/3$ ---> $Z_G=1/3$

$G(0;1/3;1/3)$

De manière analogue ... on trouve $H(2/3;0;0)$

$\overrightarrow{IG}=(0;1/3;-1/6)$

$\overrightarrow{IH}=(2/3;0;-1/2)$

$a.\overrightarrow{IG}+b.\overrightarrow{IH}=(2b/3;a/3;-a/6-b/2)$

$\overrightarrow{IK}=(1/2;1/4;-1/2)$

On a donc : 2b/3 = 1/2 ; b = 3/4
et a/3 = 1/4 ; a = 3/4

qui donne : -a/6-b/2 = -1/8 - 3/8 = -1/2

Et donc $\overrightarrow{IK}=\frac{3}{4}.\overrightarrow{IG}+\frac{3}{4}.\overrightarrow{IH}$

Calculs non vérifiés ... c'est à toi de le faire.

A comprendre absolument ... et continuer.

[hiba_mrcnn]

@Black-Jack

Le dessin c celui-ci

[Black-Jack]

@hiba_mrcnn a dit dans Question exercice géométrie dans l’espace :

@Black-Jack

Le dessin c celui-ci

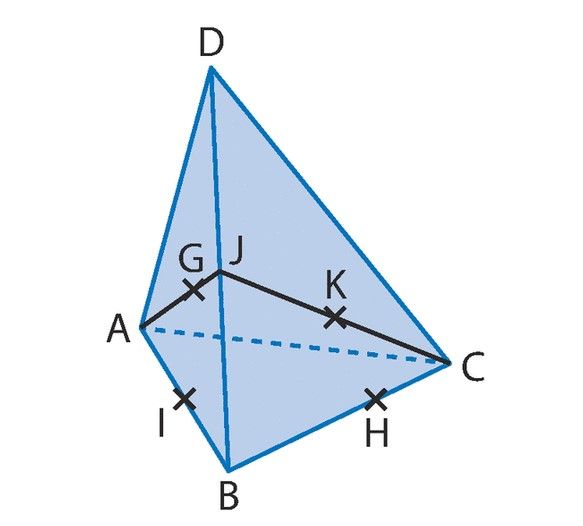
Bonjour,

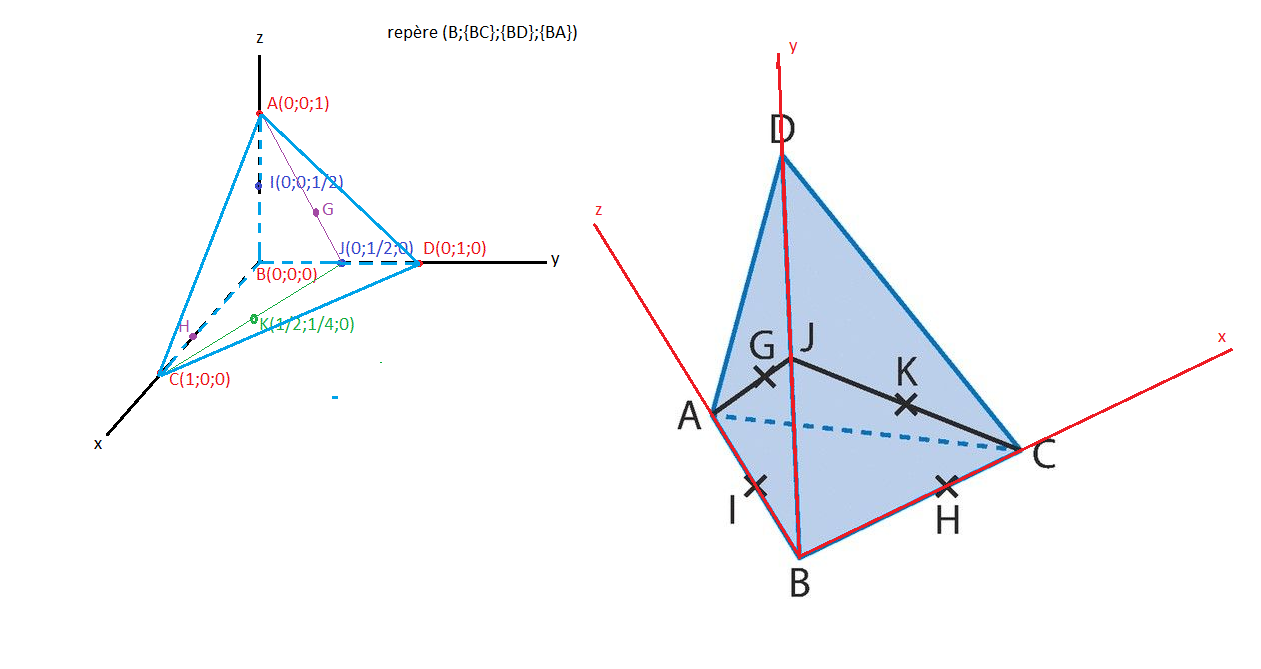
Cela ne change rien, les 2 dessins sont équivalents.

Ils sont dessinés à partir de "points d'observation" différents, mais cela ne change rien du tout pour la résolution.

Mon dessin est celui qui est le plus souvent adopté avec le repère imposé par l'énoncé ... mais on peut aussi bien utiliser l'autre dessin. C'est équivalent.

[hiba_mrcnn]

@Black-Jack

J’ai pas compris ce pour h de manière analogue ? Et pour ce que on peut en déduire

[Black-Jack]

@hiba_mrcnn a dit dans Question exercice géométrie dans l’espace :

@Black-Jack

J’ai pas compris ce pour h de manière analogue ? Et pour ce que on peut en déduire

Cela veut dire que pour trouver H, on peut utiliser la même manière de faire que celle utilisée pour trouver G.

$\overrightarrow{BC}=(1;0;0)$
$\frac{2}{3}\overrightarrow{BC}=(2/3;0;0)$
$\overrightarrow{BH}=(2/3;0;0)$
Et avec B(0;0;0) $\to$ $H(2/3;0;0)$

[hiba_mrcnn]

@Black-Jack

Pour la suite j’ai fait sa mais j’aimerai l’avoir avec les détaille avec la correction

[Black-Jack]

@hiba_mrcnn a dit dans Question exercice géométrie dans l’espace :

b)Que peut-on déduire pour les points G, H, I et K ?

b)Que peut-on déduire pour les points G, H, I et K ?

Ils sont coplanaires.
Pas demandé, mais si on veut, on peut trouver l'équation du plan, c'est : 3x + 2y + 4z = 2

[Black-Jack]

@Black-Jack a dit dans Question exercice géométrie dans l’espace :

3)a)Déterminer les représentations paramétriques des droites (IG) et (HK).

I(0 ; 0 ; 1/2)
G(0 ; 1/3 ; 1/3)
H(2/3 ; 0 ; 0)
K(1/2 ; 1/4 ; 0)

Eq paramétriques de (GI) :
$x=0$
$y-1/3=1/3\ast {\lambda }_1$
$z-1/3=-1/6\ast {\lambda }_1$

Eq paramétriques de (HK)
$x-2/3=-1/6\ast {\lambda }_2$
$y=1/4\ast {\lambda }_2$
$z=0$

Ces 2 droites sont concourantes au point D(0 ; 1 ; 0)