exercice probabilité

bonsoir j'ai un exercice que je n'arrive pas à comprendre certaines parties.
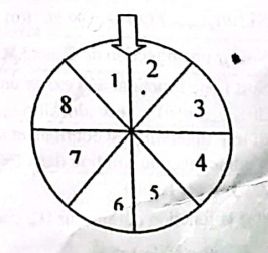
zahara découvre le jeux suivant qui consiste à rouler la roue ci contre et à choisir une des options suivantes.
Option 1: elle mise la somme de 1000F sur un nombre pair si un numéro paire sort elle gagne le double de sa mise sinon elle perd sa mise
option 2: elle mise la somme de 1000F sur un numéro si le numéro sort elle gagne 20 fois Sinon elle perd sa mise
option 3: elle mise la somme de 1000F sur les numéros 1,2,et 3 si l'un de ces numéros sort elle gagne le triple de sa mise sinon elle perd sa mise.
elle cherche à savoir la bonne option où elle aura plus de chance de gagner. à l'aide de tes connaissances mathématiques aide zahara à choisir une bonne option.
tous d'abord j'ai commencé à déterminer les valeurs prises par la variable aléatoire X ( la variable aléatoire est le gain qu'elle va gagner) sont 2000F; -1000F; 20000F et 3000F. P(20000)=1/2. j'ai du mal à calculer les autres probabilité et à avancer dans mon exercice

@jean-12 Bonjour,

Pour le calcul des probabilités, il faut avoir la roue ou les nombres que comporte cette roue.

@Noemi bonjour

@jean-12

Combien de choix possibles :
si on choisit un nombre pair : 4 possibilités parmi 8, donc la probabilité :
P(gain 2000) = \dfrac{4}{8}= ...$
Si on choisit un nombre parmi 1, 2 et 3, : 3 possibilités parmi 8, donc .....

@Noemi bonjour
les valeurs prises par la variable aléatoire X ( la variable aléatoire est le gain qu'elle va gagner) sont 2000F; -1000F; 20000F et 3000F. P(gain=20000)=1/2 ,
Si on choisit un nombre parmi 1, 2 et 3, : 3 possibilités parmi 8, donc la probabilité est 3/8

@jean-12
C'est faux pour le gain de 20000, car une seule possibilité.

@Noemi
d'accord mais mes autres probabilité sont elles exacte ?

@jean-12
donc P(20000)=1/8

@jean-12

C'est juste.

@Noemi maintenant pour trouver la meilleure option je prends la plus grande probabilité

@jean-12

Oui s'il s'agit d'avoir le bon numéro.

@Noemi donc la première option qui est la bonne car c'est la plus grande probabilité

@jean-12

Oui, les nombres pairs.