Fonctions. numériques
-
MMMounah dernière édition par
Bonsoir
On considère la fonction f de la variable réelle w. Définie par : f(x) = { e^(1/lnx) ; x # 0 et x # 1
{ 1 ; si x = 0
{ 0; si x = 1
NB: (# = différent)- Étudier la continuité de f en 0 et en 1 .
Et quel est l’ensemble de définition svp
- Étudier la continuité de f en 0 et en 1 .
-
@Zeïnab-Mahamadou Bonjour,
Indique tes éléments de réponse.
Calcule la limite lorsque xxx tend vers 0 et vers 1.
-
MMMounah dernière édition par
@Noemi L’ensemble de définition c’est R ?
La limite je ne sais pas quel f(x) utiliser ?
-
BBlack-Jack dernière édition par
@Zeïnab-Mahamadou a dit dans Fonctions. numériques :
@Noemi L’ensemble de définition c’est R ?
La limite je ne sais pas quel f(x) utiliser ?Bonjour,
NON
-
@Zeïnab-Mahamadou
Utilise f(x)=e1ln(x)f(x)= e^{\frac{1}{ln(x)}}f(x)=eln(x)1
ln(x)ln(x)ln(x) est définie si xxx est .....
-
MMMounah dernière édition par
@Black-Jack bonsoir
C’est quoi l’ensemble de définition alors
-
MMMounah dernière édition par
@Noemi bonsoir
Si quoi ?
J’ai rien compris
Je dois utiliser à limite à quand x tend vers 0+ et 0-?Si ouii comment ? Sinon expliquez moi
-
@Zeïnab-Mahamadou
Regarde ce cours : https://www.mathforu.com/terminale-s/fonctions-exponentielles-et-logarithme-pour-terminale-s/
-
MMMounah dernière édition par
@Noemi merci
-
MMMounah dernière édition par
@Zeïnab-Mahamadou
Df= ]o;1[U]1;+oo[
f est n’est pas continue en 0 et n’est pas continue en 1 ? C’est ça ?
-
@Zeïnab-Mahamadou
Oui pour le domaine de définition.
Pour la continuité, as-tu calculé les limites ?
-
MMMounah dernière édition par
@Zeïnab-Mahamadou
2. Étudier la derivabilité de f en 0 et 1 . Interpréter géométriquement
3.Étudier les variations de f et tracer sa courbe (C) dans un plan muni d’un repère orthonormé (O;i; j)
4.A l’aide de la question précédente, représenter l’ensemble des points M(X;Y) tels que : ln|x| x ln|y| = 1
-
MMMounah dernière édition par
@Noemi
Oui la première = 1 et la 2eme =+oo ?
Et
Comment écrire en latex svp
-
MMMounah dernière édition par
@Zeïnab-Mahamadou pour la dérivablité
lim [(e^1/lnx )-1]/x ? Décortiquer le moii svp
x—>0
-
MMMounah dernière édition par
@Zeïnab-Mahamadou
@Noemi @Black-Jack répondez svp
-
@Zeïnab-Mahamadou
Si tu souhaites t'initier au Latex, tu peux consulter ici :
https://forum.mathforu.com/topic/163/comment-écrire-les-principales-expressions-mathématiques-work-in-progressPour la limite, utilise la règle de l'Hospital.
-
MMMounah dernière édition par
@Noemi je parle de cette question
Ensuite pour question 3)
la dérivée de e^(1/lnx) c’est - [e^1/lnx] /[x(lnx)^2] ? Si oui son signe
-
MMMounah dernière édition par
@Noemi et c’est quoii la règle de L’hôpital ?
-
BBlack-Jack dernière édition par
@Noemi a dit dans Fonctions. numériques :
@Zeïnab-Mahamadou
Oui pour le domaine de définition.
Pour la continuité, as-tu calculé les limites ?Bonjour Noemi,
Zeïnab Mahamadou a ecrit : Df= ]0;1[U]1;+oo[
Je pense qu'on ne peut pas exclure 0 du domaine tant qu'on n'a pas
vérifié si lim(x-->0+) e^(1/ln(x)) était ou non égale à f(0) = 1 (donné dans l'énoncé)Si on trouve bien lim(x-->0+) e^(1/ln(x)) = 1
comme l'énoncé précise que f(0) = 1, je pense que 0 doit être compris dans DfL'ordre des questions de l'énoncé (d'abord étudier la continuité en 0 et en 1 et ensuite déterminer Df) est impératif.
-
BBlack-Jack dernière édition par Black-Jack
@Zeïnab-Mahamadou a dit dans Fonctions. numériques :
@Noemi et c’est quoii la règle de L’hôpital ?
Bonjour,
La règle de Lhospital n'est pas, je pense , au programme de Terminale.
Sauf si cela a changé.
-
MMMounah dernière édition par
@Black-bonsoir
On a pas demandé Df dans l’énoncé, j’ai juste posé la question pour savoir
-
BBlack-Jack dernière édition par
@Zeïnab-Mahamadou a dit dans Fonctions. numériques :
@Black-bonsoir
On a pas demandé Df dans l’énoncé, j’ai juste posé la question pour savoirBonjour,
OK, mais si tu l'as demandé; je présume que tu es intéressé par le sujet.
Et je pense que le Df que tu as indiqué , soit : Df= ]0;1[U]1;+oo[ n'est pas correct.
Pour corriger, il faut commencer par étudier la continuité de f en 0 et en 1 .
-
@Zeïnab-Mahamadou
Le domaine de définition indiquée est celui de la fonction : f(x)=e1ln(x)f(x)= e^{\frac{1}{ln(x)}}f(x)=eln(x)1
Pour la limite, utilise la notion de nombre dérivée.
-
MMMounah dernière édition par
@Black-Jack bonsoir
Donc en gros Df = [0;+oo[
Je m’explique Df=]0;1[U]1;+oo[ U {0} U {1}
= [0;+oo[
-
MMMounah dernière édition par
@Black-Jack bonsoir
f est continue en 0 à droite et n’est pas continue en 1
-
MMMounah dernière édition par
@Zeïnab-Mahamadou alors la dernière question 4.) je fais comment svp ?
-
MMMounah dernière édition par
@Black-Jack la dérivablité en 0 la çà. Donc combien svp détailler moi.
Je suis sur cet exo depuis le matin et j’ai n’ai eu aucun résultat concret jusque là
-
BBlack-Jack dernière édition par
@Zeïnab-Mahamadou a dit dans Fonctions. numériques :
@Black-Jack bonsoir
f est continue en 0 à droite et n’est pas continue en 1Bonjour,
Ca c'est pour moi correct.
-
BBlack-Jack dernière édition par
Rebonjour,
f'(x) = -[e^(1/lnx)] /[x(lnx)^2]
f'(x) --> -oo pour x --> 0+
f'(x) < 0 pour x dans ]0 1[ --> f est décroissante.
lim(x--> +1-) f'(x) = 0 (et f(x) --> 0)
lim(x--> +1+) f'(x) = -oo (et f(x) --> +oo)
Il y a donc discontinuité de f pour x = 1
f'(x) < 0 pour x > 1 --> f est décroissantedessiner graphique ...
Si j'interprète bien la question. (ce qui n'est pas sur).
M(X ; Y)
X = x et Y = e^(1/lnx)
ln|y| = ln|e^(1/lnx)|Pour x dans ]0 ; 1[ ln(x) < 0 ln|y| = 1/ln(x)
ln|x|.ln|y| = ln(x) * 1/ln(x) = 1 , tous les points de f d'abscisse dans ]0 ; 1[ conviennent comme point MPour x dans ]1 ; oo[ ln(x) > 0 ln|y| = 1/ln(x)
ln|x|.ln|y| = ln(x) * 1/ln(x) = 1 toujours vérifié, tous les points de f d'abscisse > 1 conviennent comme point MDonc tous les points de f d'abscisses dans ]0 ; 1[ U ]1 ; oo[ conviennent comme points M.
Réfléchir encore pour le point de f d'abscisse 0...
-
MMMounah dernière édition par
@Black-Jack bonsoir svp transformer ça en latex pour mieux comprendre
-
BBlack-Jack dernière édition par
@Zeïnab-Mahamadou a dit dans Fonctions. numériques :
@Black-Jack bonsoir svp transformer ça en latex pour mieux comprendre
Bonjour,
Je te laisse le soin de le faire ...
Ou bien de ne pas tenir compte de ma réponse si elle ne te plait pas.
-
MMMounah dernière édition par
@Black-Jack bonjour comment le transformer alors ?
Et tu parles de quelle réponse
-
mtschoon dernière édition par mtschoon

Bonjour, je ne fais que passer.
@Zeïnab-Mahamadou je n’ai pas suivi tout ce long topic, et Black-Jack répondra à ta dernière question s’il le souhaite.
je me contente de regarder la formulation de tes questions.Pour la question 1), ton professeur ne l'aurait pas formulée ainsi ! ! !
(tu as indiqué que c'était ta rédaction)
C’est un non-sens d’étudier continuité ou autre propriété avant de déterminer de domaine de définition .Même si ce n’est pas demandé , pour toute fonction numérique f de variable réelle x, il faut savoir pour qu’elles valeurs de x l’expression f(x) est calculable , pour pouvoir légitimer les calculs.
Cela revient à déterminer le domaine DfD_fDf de définition de la fonction.
Ensuite, tous les calculs utiles, pour limites, continuité, dérivabilié etc, sont faits avec x∈Dfx\in D_fx∈Df.Je te détaille une explication de DfD_fDf, que tu as peut-être faite...
Dans ton énoncé, l’expression f (x) est exprimée dans 3 cas disjoints.
Tu cherches les conditions d’existence de f(x) dans chacun des 3 cas.1er cas :
Pour x=0, alors f(x)=1 c’est à dire f(0)=1 . Donc 0∈Df0 \in Df0∈Df2ème cas :
Pour x=1, alors f(x)=0 c’est à dire f(1)=0 Donc 1∈Df1 \in Df1∈Df3eme cas : x≠0x\ne 0x=0 et x≠1x\ne 1x=1, c’est à dire x∈Rx \in Rx∈R \{0,1}
f(x)=e1ln(x)f(x)=e^{\dfrac{1}{ln(x)}}f(x)=eln(x)1
Les deux conditions sont :
x>0x\gt 0x>0 pour de ln(x)ln(x)ln(x) existe
x≠1x\ne 1x=1 pour que ln(x)ln(x)ln(x) soit non nul (car on ne peut pas diviser par 0)
En bref, dans ce 3ème cas, f(x) est calculable pour x∈]0,1[∪]1,+∞[x\in ]0,1[\cup ]1,+\infty[x∈]0,1[∪]1,+∞[En faisant la réunion des 3 cas, tu obtiens : Df=[0,+∞[\boxed{D_f=[0,+\infty[}Df=[0,+∞[ (je crois que tu l’as trouvé)
-
mtschoon dernière édition par

@Zeïnab-Mahamadou , pour vérification éventeulle, je te joins la représentation graphique ( parties en BLEU) de fff
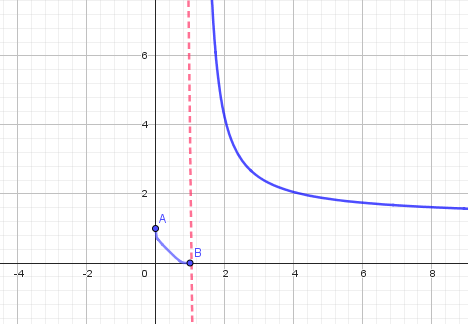
-
mtschoon dernière édition par mtschoon

@Zeïnab-Mahamadou , pour la dernière question, si j'ai bien lu, à l’aide de la représentation graphique de fff, tu dois représenter l’ensemble des points M(x,y)M(x,y)M(x,y) tels que : ln∣x∣×ln∣y∣=1ln|x| \times ln|y| = 1ln∣x∣×ln∣y∣=1
Je te joins un schéma de cette représentation graphique
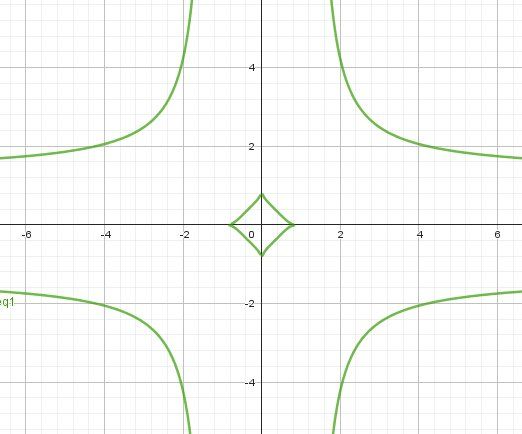
Evidemment, il faut le justifier.
Piste à creuser ( ce n'est qu'une piste) :
L'expression ln∣x∣×ln∣y∣ln|x| \times ln|y|ln∣x∣×ln∣y∣ est définie pour x≠0x\ne 0x=0 et y≠0y\ne 0y=0
De plus, pour ∣x∣≠1|x|\ne 1∣x∣=1 : ln∣y∣=1ln∣x∣ln|y|=\dfrac{1}{ln|x|}ln∣y∣=ln∣x∣1 <=> ∣y∣=e1ln∣x∣|y|=e^{\dfrac{1}{ln|x|}}∣y∣=eln∣x∣1En fonction des signes de xxx et de yyy, cette dernière égalité se transforme et tu dois en déduire des symétries (par rapport aux axes de coordonnées ou au point origine) pour la construction de cet ensemble de points MMM en partant de la représentation graphique de fff.
Bon travail !