Géométrie synthétique - quadrilatères

[-lala-o]

Bonjour, voici 2 exercices que j'ai réalisé. Je ne suis pas certaine de les avoir réalisés de la bonne manière, alors j'aimerais avoir confirmation que je n'ai pas fait n'importe quoi. Voila les énoncés et mes réponses :

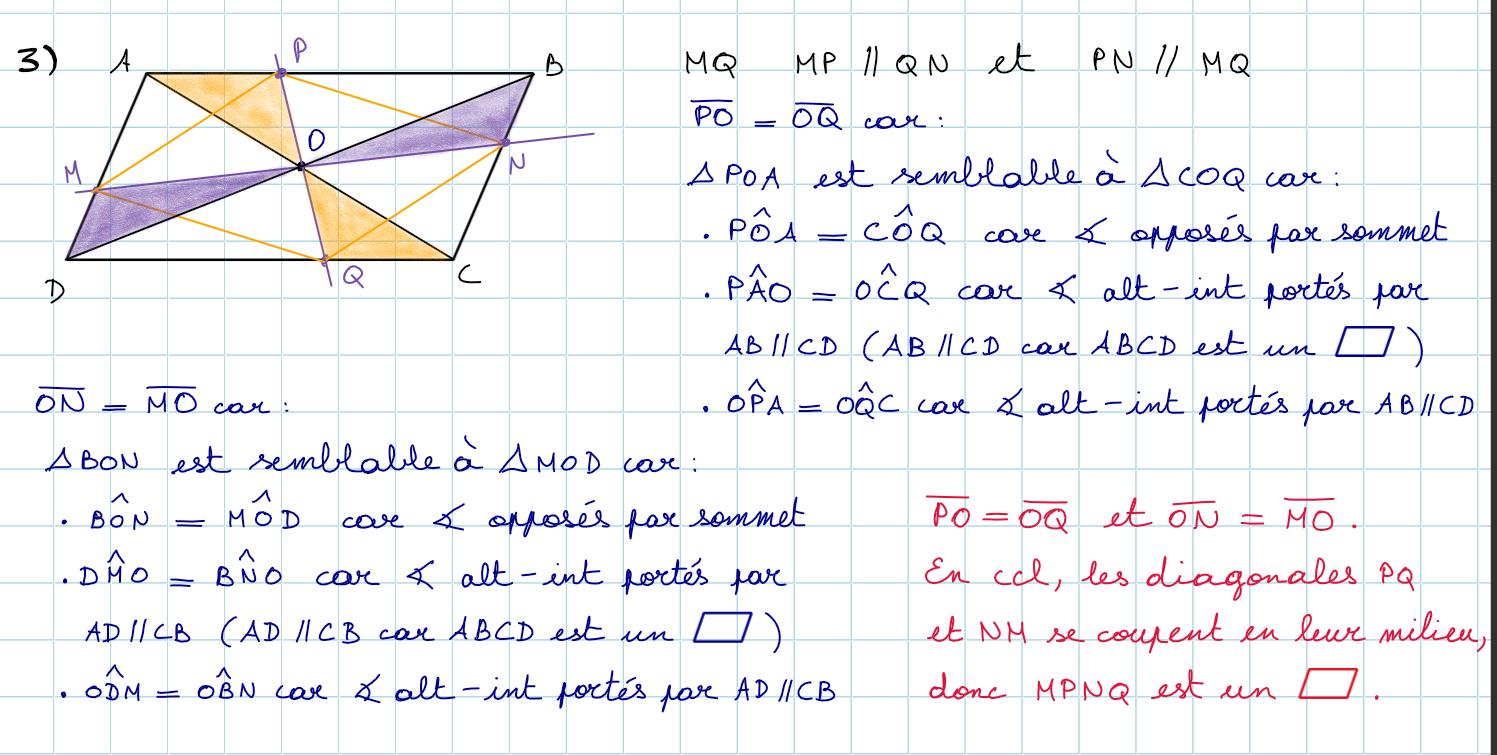
Soit le parallélogramme ABCD et O = Intersection de AC et BD. Par O, on mène une première droite qui coupe AB en P et DC en Q et une deuxième droite qui coupe AD en M et BC en N.
Démontre que le quadrilatère MPNQ est un parallélogramme.

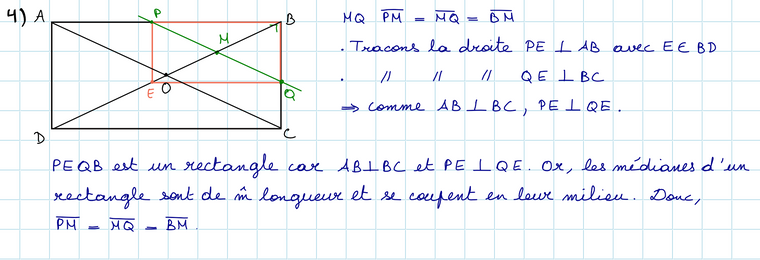
Soit un rectangle ABCD de centre O (intersection des diagonales). Par P, un point quelconque pris sur [AB], on trace PQ parallèle à AC qui rencontre BD en M.
Montre que |PM| = |MB| = |MQ|.

[Noemi]

@srhmrc Bonjour,

Attention, un seul exercice par post. Propose un autre sujet pour le deuxième exercice.

Pour le premier, il manque dans la démonstration le fait que le point $O$ est le milieu des diagonales.
Deux triangles semblables ne sont pas obligatoirement identiques.