Problème de seuil et footeux

Bonjour à tous,

voici un nouvel exercice sur le thème du moment à savoir la loi binomiale.
J'ai un petit doute sur l'interprétation de mes résultats.
Pourriez-vous me dire si j'ai des raisons d'être dubitatif ?
Merci par avance

Enoncé

Un footeux aura une prime s'il reçoit $n$ cartons jaunes ou moins sur les 38 matchs de la saison. La probabilité $p$ qu'il prenne un carton jaune au cours d'un match est de 0.15.

Quelle est la + petite valeur de $n$ pour qu'il soit sûr au seuil de 99% de toucher cette prime ?
Même question avec un risque de ne pas recevoir la prime inférieur à 10%.

Mes réponses

La variable $n$ étant attribuée au nombre de carton on prendra la variable $m$ pour le nombre de match.
On a donc la loi binomiale avec la variable aléatoire $X$ associée au nombre $n$ ( $n$ = nombre de carton jaune)

On a donc $\sim B (38 ; 0.15)$

$P(X≤10)=0,9793P(X\le10)=0,9793$ et $P(X≤11)=0,9923P(X\le11)=0,9923$
Il faut donc qu'il ait moins de 11 cartons jaunes pour toucher la prime (avec une certitude de 99%)
Le nombre $n$ pour que le risque de ne pas recevoir la prime soit inférieur à 10% est le même pour que les chances de recevoir la prime soit de 90%.

$P(X≤8)=0,8943P(X\le8)=0,8943$ et $P(X≤9)=0,9505P(X\le9)=0,9505$
Il lui faut avoir moins de 9 cartons jaunes pour que le risque de ne pas recevoir sa prime soit inférieur à 10%.

@Chris21300 Bonjour,

Tu es sur de l'énoncé : la plus petite valeur de $n$ ?
C'est $n = 0$ .

l'énonvé m'a effectivement interloqué @Noemi....
En fait je travaille sur plusieurs livre de spécialité mathématique notamment le Barbazo ainsi que le Magnard ...
Je sais que les photographies sont interdites donc je vais essayer de t'envoyer en MP l'énoncé du problème ?

en fait je ne sais pas comment envoyer un MP @Noemi...
Du coup je te joins ici la photo de l'énoncé )

@Chris21300

Peut-être une erreur d'énoncé, réfléchi avec la plus grande valeur de $n$ .

@Noemi
@Noemi
bah j'ai fait le calcul avec la variable m = 38 du coup vu que la variable n était affectée au nombre de carton jaune ... et donc j'ai fait comme si on cherchait un nombre de match et non pas de cartons jaunes ? Tu penses que c'est cela qu'"il fallait faire ?

@Chris21300

On ne peut avoir qu'un carton jaune par match, donc c'est correct.

je m'emmelle complètement les pinceaux là @Noemi

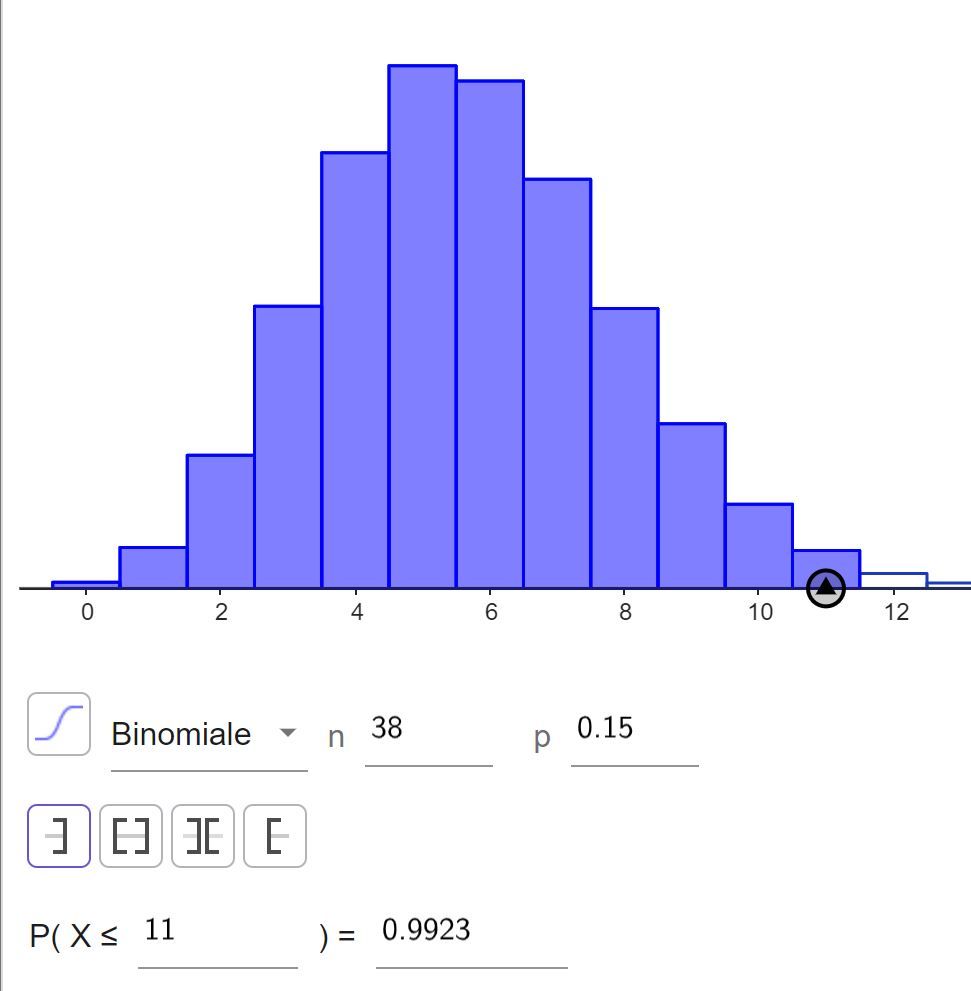
Comment est ce que j'interprète cela ?
J'ai 99% de chance de n'obtenir qu'un seul carton jaune si je fais moins de 11 match c'est bien cela ?

@Chris21300

Il faut chercher $k$ tel que $p(X≥k)≥0,99p(X\geq k)\geq0,99$ .

@Noemi

excuse moi d'insiter mais avant de corriger mon erreur (tu m'as dit dans le message précédent de faire un autre calcul) je voudrais avoir ton aide sur mon interrogation précédente ...
est ce que l'interprétation du graphique ci joint est : J'ai 99% de chance de n'obtenir qu'un seul carton jaune si je fais moins de 11 match .

@Noemi a dit dans Problème de seuil et footeux :

@Chris21300

Il faut chercher $k$ tel que $p(X≥k)≥0,99p(X\geq k)\geq0,99$ .

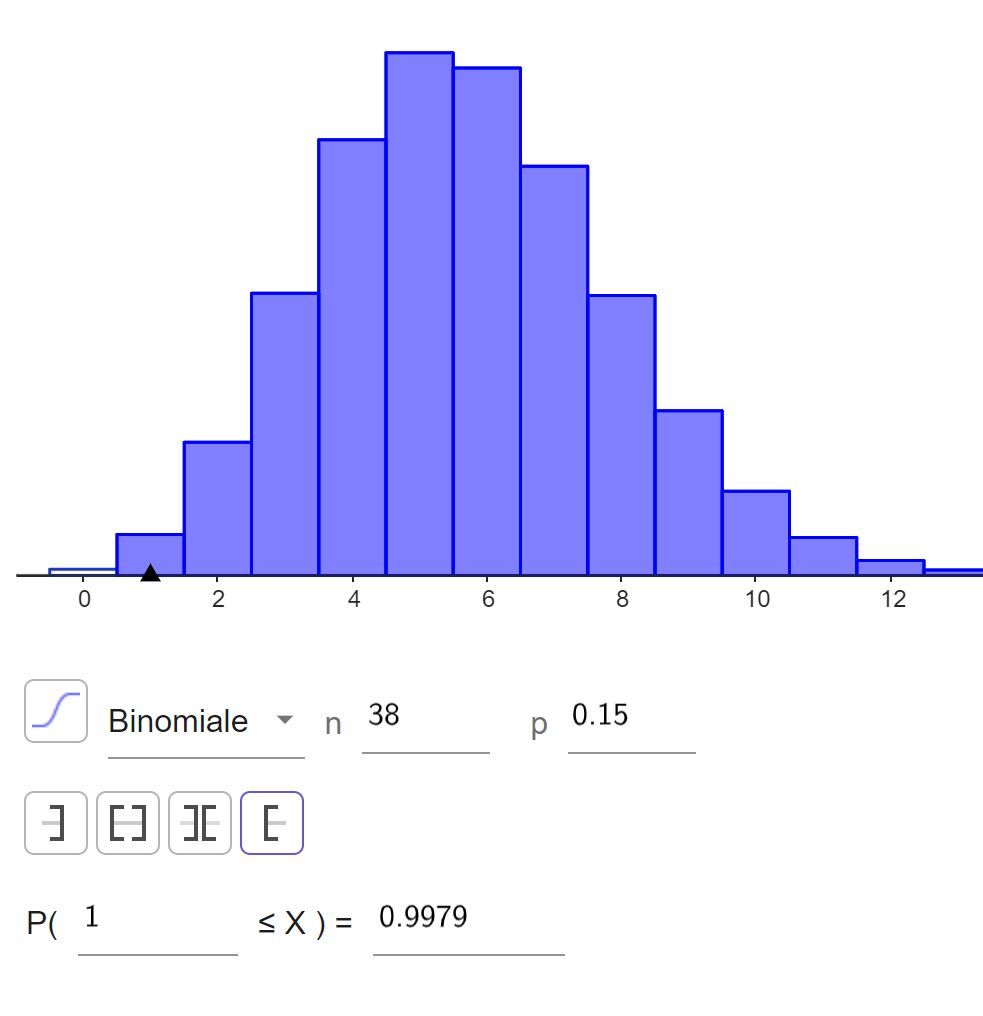
Je trouve alos $p(X≥1)≥0,99p(X\geq 1)\geq0,99$ .
et donc il faudrait faire au moins un match pour être quasiment sûr d'avoir la prime c'erst cela ?

@Chris21300

Pour être sur de toucher la prime, il faut qu'il ne prenne qu'un seul carton jaune.