Problème de seuil et élections

[Chris21300]

Enoncé

Le candidat A a obtenu 20,01% des suffrages à une élection.
On considère un sondage sur 1000 personnes réalisé avant cette élection et $F$ la variable aléatoire donnant la fréquence d'intention de vote pour A dans ce sondage.

1. Déterminer un intervalle de la forme $[0;f]$ le + petit possible tel que $p(F\in [0;f])\ge 0.99$

2. L'année précédente, la plupart des sondages créditait A d'au-moins 25% d'intention de vote puis juste avant l'élection ils le créditent d'entre 17% et 21% d'intention de vote. Que peut-on en penser ?

Mes réponses

Un nouvel exercie qui débute bien mal puisque justement je n'arrive pas à le débuter...
Dois je commencer par calculer un intervalle de fluctuation au seuil de 99% ?
Si oui, après avoir vérifié mes critères de validité ($n=1000$ et $p=0.2001$ j'obiens :

$I_{1000}=[0.167;0.232]$

Ce qui signifie qu'entre 16,7% et 23,2% des sondés envisagent de voter pour A (avec une marge d'erreur de 1%).

Je ne sais pas si ce que je viens de faire a une utilté mais j'avoue ne pas savoir où aller pour cette question

Je suis bien évidemment preneur du moindre conseil pour avancer dans cet exercice
Merci par avance ...

[Noemi]

@Chris21300 Bonjour,

Oui pour le calcul de l'intervalle de fluctuation. Pour la réponse, il faut tenir compte de l'énoncé de la question qui indique la valeur de la borne inférieure de l'intervalle.

[Chris21300]

@Noemi

On sait que $P(F\in [a;b])=P(a\le F\le b)$ donc si on a $P(F\in [0;f])\ge 0.99$ je dois trouver
$f$ tel que $P(F\le f)\ge 0.99$ ?

[Noemi]

@Chris21300

Oui

[Chris21300]

Bon je termine cet exercice et après repos parce que ça commence à chauffer là haut @Noemi

Donc pour trouver $f$ tel que $P(F\le f)\ge 0.99$ j'utilise geogebra et j'obtiens cela :

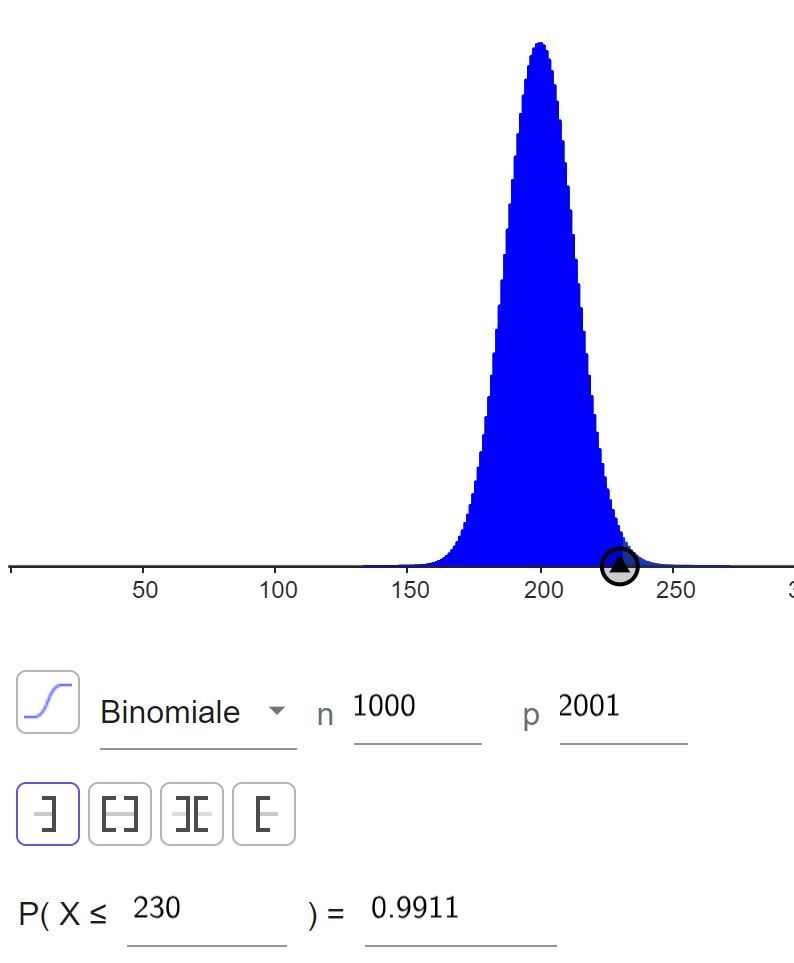
Comme je cherche une fréquence je divise le nombre d'individus par l'effectif de l'échantillon et j'obtiens une une fréquence de 0.23 ?

Donc $P(F\le 0.23)\ge 0.99$

Si cela est bon, comment interpréter ce résultat ?
On estime qu'au moins 23% des personnes voteront pour le candidat avec un risque d'erreur de 1% ?

[Chris21300]

@Noemi
Et donc concernant la 2° question il n'y a pas de calcul à faire j'imagine ?
Il suffit de dire que les sondages sont d'autant plus proches de ce que sera le résultat final au fur et à mesure qu'on se rapproche du jour de l'élection ?

[Noemi]

@Chris21300

Oui, la question 2 est juste une analyse que l'on peut interpréter de différentes façon.