Autre probleme se géométrie 3 eme

BONJOUR
Encore besoin d aide
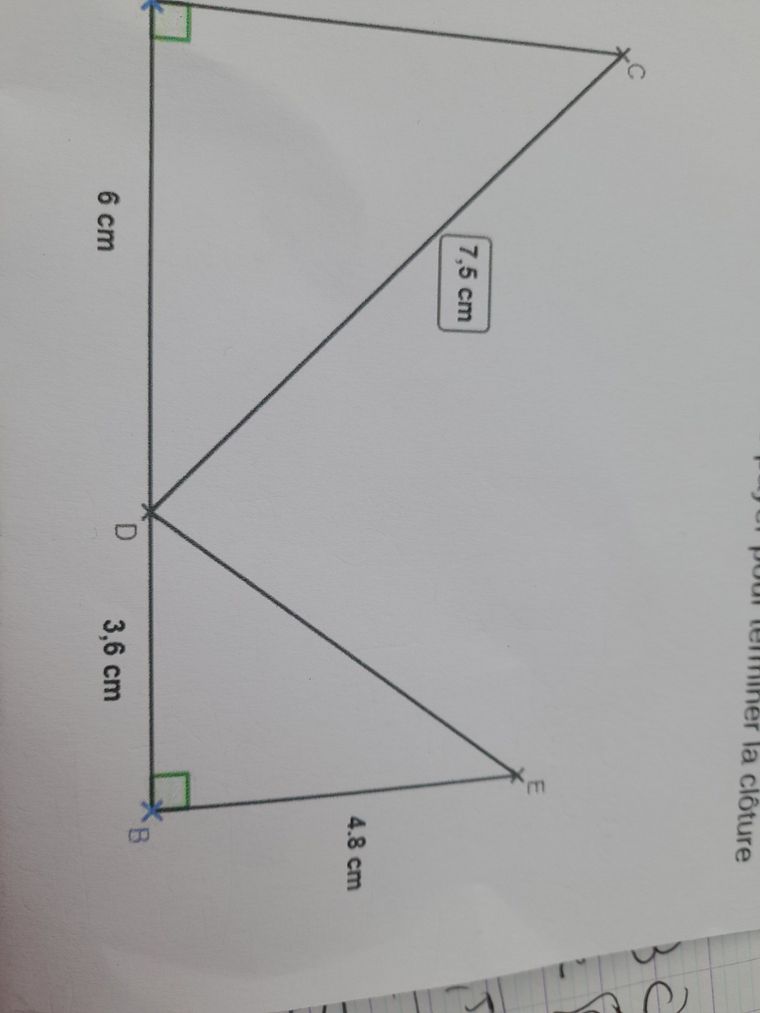
Je vous remercie d avance

Sur la figure ci dessous
Le triangle ACD EST RECTANGKE EN A
Le triangle BDE rectangle en B
Les points AB D sont alignés

1 CALCULER les longueurs AC et DE

2 montrer que ACD et BDE sont semblables

3 on note x la mesure de l angle ADC
A. Exprimer en fonction de X la mesure de l angle BDE puiiis expliquer pourquoi CDE = 90°

B. Le triangle CDE est il semblable aux triangles ACD et CDE

![text alternatif](url de l'image)

@m12 Bonjour,

Indique tes calculs et la question qui te pose problème.
1, Utilise le théorème de Pythagore.

@Noemi a dit dans Autre probleme se géométrie 3 eme :

@m12 Bonjour,

Indique tes calculs et la question qui te pose problème.
1, Utilise le théorème de Pythagore.

Pour AC

AC2= cD2-AB2
AC2 = 7.5 AU CARRE - 6 AU CARRE
AC2 = 56.25 - 36
AC RACINE CARRE DE 20.25

AC = 4.5 CM

@m12

C'est juste.
Poursuis tes calculs, je vérifierai ce soir.

@Noemi a dit dans Autre probleme se géométrie 3 eme :

@m12

C'est juste.
Poursuis tes calculs, je vérifierai ce soir.

Pour DE2=DB AU CARRE+EB AU CARRE
DE2=3.6 AU CARRE+ 4.8 AU CARRE

DE = 6 CM

@Noemi a dit dans Autre probleme se géométrie 3 eme :

@m12

C'est juste.
Poursuis tes calculs, je vérifierai ce soir.

Pour la question 2
Les triangles ACD ET BDE sont semblables car
AC=BE
BE=DB
ANGLE CAD ET ANGLE EBD SONT EGAUX

JE vous pas autre chose

@Noemi a dit dans Autre probleme se géométrie 3 eme :

@m12

C'est juste.
Poursuis tes calculs, je vérifierai ce soir.

Pour ls question 3 je comprends pas

@m12

Pour la question 2, il faut calculer les rapports des côtés.
$DBAC=....\dfrac{DB}{AC}= ....$

$BEAD=....\dfrac{BE}{AD}= ....$
et
....

Pour la question 3,
Vu que les triangles sont semblables,
indique les angles qui sont égaux.
La somme des angles d'un triangle est égale à ......°.
Un angle plat a pour mesure ....°.

@Noemi a dit dans Autre probleme se géométrie 3 eme :

@m12

Pour la question 2, il faut calculer les rapports des côtés.
$DBAC=....\dfrac{DB}{AC}= ....$

$BEAD=....\dfrac{BE}{AD}= ....$
et
....

Pour la question 3,
Vu que les triangles sont semblables,
indique les angles qui sont égaux.
La somme des angles d'un triangle est égale à ......°.
Un angle plat a pour mesure ....°.

DB/AC=3.6/4,5
BE/AD=4.8/6
ET CD/DE= 7.5 /6

@Noemi a dit dans Autre probleme se géométrie 3 eme :

@m12

Pour la question 2, il faut calculer les rapports des côtés.
$DBAC=....\dfrac{DB}{AC}= ....$

$BEAD=....\dfrac{BE}{AD}= ....$
et
....

Pour la question 3,
Vu que les triangles sont semblables,
indique les angles qui sont égaux.
La somme des angles d'un triangle est égale à ......°.
Un angle plat a pour mesure ....°.

180°
90°

C'est ça?

@m12

Fais les calculs pour vérifier que les rapports sont égaux.
Le dernier rapport est faux, c'est
$DEDC=....\dfrac{DE}{DC}= ....$

@Noemi a dit dans Autre probleme se géométrie 3 eme :

@m12

Fais les calculs pour vérifier que les rapports sont égaux.
Le dernier rapport est faux, c'est
$DEDC=....\dfrac{DE}{DC}= ....$

Je trouve 0.8 pour les 3 donc triangles egaux

@m12

Donc triangles semblables.

@Noemi a dit dans Autre probleme se géométrie 3 eme :

@m12

Donc triangles semblables.

Oui

Et pour le petit b de la question 3 je comprends pas
Le triangle cde est pas semblable c'est pas un triangle ?

@m12

Pour la question 3, fais d'abord le a).
Tu peux tracer le segment $C E$ pour voir le triangle $C D E$ .

@Noemi a dit dans Autre probleme se géométrie 3 eme :

@m12

Pour la question 3, fais d'abord le a).
Tu peux tracer le segment $C E$ pour voir le triangle
C'est fait mais je vois pas se qu il faut faire

@m12

$ADC^=x\widehat{ADC}=x$
Vu que les triangles sont semblables $ADC^=DEB^\widehat{ADC}=\widehat{DEB}$
et
$DEB^+BDE^=90°\widehat{DEB}+\widehat{BDE}=90°$
donc
$BDE^=....\widehat{BDE}=....$

@Noemi a dit dans Autre probleme se géométrie 3 eme :

@m12

$ADC^=x\widehat{ADC}=x$
Vu que les triangles sont semblables $ADC^=DEB^\widehat{ADC}=\widehat{DEB}$
et
$DEB^+BDE^=90°\widehat{DEB}+\widehat{BDE}=90°$
donc
$BDE^=....\widehat{BDE}=....$

DONC BDE = 45°
Si J ai bien compris

@m12 a dit dans Autre probleme se géométrie 3 eme :

@Noemi a dit dans Autre probleme se géométrie 3 eme :

@m12

$ADC^=x\widehat{ADC}=x$
Vu que les triangles sont semblables $ADC^=DEB^\widehat{ADC}=\widehat{DEB}$
et
$DEB^+BDE^=90°\widehat{DEB}+\widehat{BDE}=90°$
donc
$BDE^=....\widehat{BDE}=....$

DONC BDE = 45°
Si J ai bien compris

Et donc Cde = 90° car angle bde = 45 et cda =45

@m12

Non

$ADC^=x\widehat{ADC}=x$
Vu que les triangles sont semblables $ADC^=DEB^\widehat{ADC}=\widehat{DEB}$
et
$DEB^+BDE^=90°\widehat{DEB}+\widehat{BDE}=90°$
donc
$BDE^=90°−DEB^=90°−x\widehat{BDE}=90° - \widehat{DEB} = 90° - x$
l'angle $ADB^=180°\widehat{ADB} = 180°$ angle plat
donc $ADC^+CDE^+EDB^=180°\widehat{ADC}+\widehat{CDE}+\widehat{EDB}= 180°$
Soit $CDE^=180°−(90°−x)−x=....\widehat{CDE}=180°-(90°-x)-x= ....$
donc $CDE^=.....\widehat{CDE}= .....$

b) Pour vérifier si les triangles sont semblables calcule $C E$ puis les rapports des côtés.

@Noemi a dit dans Autre probleme se géométrie 3 eme :

@m12

Non

$ADC^=x\widehat{ADC}=x$
Vu que les triangles sont semblables $ADC^=DEB^\widehat{ADC}=\widehat{DEB}$
et
$DEB^+BDE^=90°\widehat{DEB}+\widehat{BDE}=90°$
donc
$BDE^=90°−DEB^=90°−x\widehat{BDE}=90° - \widehat{DEB} = 90° - x$
l'angle $ADB^=180°\widehat{ADB} = 180°$ angle plat
donc $ADC^+CDE^+EDB^=180°\widehat{ADC}+\widehat{CDE}+\widehat{EDB}= 180°$
Soit $CDE^=180°−(90°−x)−x=....\widehat{CDE}=180°-(90°-x)-x= ....$
donc $CDE^=.....\widehat{CDE}= .....$

b) Pour vérifier si les triangles sont semblables calcule $C E$ puis les rapports des côtés.

Donc CDE= 90 °

@m12

Oui
$180 - 90 + x - x = 90$

@Noemi a dit dans Autre probleme se géométrie 3 eme :

@m12

Oui
$180 - 90 + x - x = 90$

Yesssss

@Noemi a dit dans Autre probleme se géométrie 3 eme :

@m12

Non

$ADC^=x\widehat{ADC}=x$
Vu que les triangles sont semblables $ADC^=DEB^\widehat{ADC}=\widehat{DEB}$
et
$DEB^+BDE^=90°\widehat{DEB}+\widehat{BDE}=90°$
donc
$BDE^=90°−DEB^=90°−x\widehat{BDE}=90° - \widehat{DEB} = 90° - x$
l'angle $ADB^=180°\widehat{ADB} = 180°$ angle plat
donc $ADC^+CDE^+EDB^=180°\widehat{ADC}+\widehat{CDE}+\widehat{EDB}= 180°$
Soit $CDE^=180°−(90°−x)−x=....\widehat{CDE}=180°-(90°-x)-x= ....$
donc $CDE^=.....\widehat{CDE}= .....$

b) Pour vérifier si les triangles sont semblables calcule $C E$ puis les rapports des côtés.

Pour le b

J ai calculé CE = 6+3.6 = 9.6

Rapport DE/AD
cd/ eb
Ce/ca
Les résultats sont pas les mêmes donc cesr pas un triangle semblable

@m12

Pour le calcul de $C E$ , il faut appliquer le théorème de Pythagore.

Oui, Les rapports ne sont pas égaux, donc ces triangles ne sont pas semblables.

@Noemi a dit dans Autre probleme se géométrie 3 eme :

@m12

Pour le calcul de $C E$ , il faut appliquer le théorème de Pythagore.

Oui, Les rapports ne sont pas égaux, donc ces triangles ne sont pas semblables.

CE au carré = CD au carré + De au carré
CE = 9.6

@m12

C'est une valeur approchée,
$C E = 9, 6046 . . . .$

@Noemi a dit dans Autre probleme se géométrie 3 eme :

@m12

C'est une valeur approchée,
$C E = 9, 6046 . . . .$

OK
Merci pour toutes vos explications

@m12

C'est parfait si tu as tout compris.

@Noemi a dit dans Autre probleme se géométrie 3 eme :

@m12

C'est une valeur approchée,
$C E = 9, 6046 . . . .$

J ai bien trouvé 9.6 pour CE

Par contre les rapport pour prouver que CDE c'est oui ou non un triangle semblables
Est ce cela
CE/CA 9.6/4.5
CD/DB 7.5/ 3.6
ED/ AD 6/6

@m12

Tu choisis les triangles en faisant correspondre les angles.
Triangles $A C D$ et $D E C$ .

@Noemi a dit dans Autre probleme se géométrie 3 eme :

@m12

Tu choisis les triangles en faisant correspondre les angles.
Triangles $A C D$ et $D E C$ .

Oh la la
C'est donc bon ce que j'ai fais?

@m12

Non,

Vérifie les rapports que tu as écrits.

@Noemi a dit dans Autre probleme se géométrie 3 eme :

@m12

Non,

Vérifie les rapports que tu as écrits.

CE/CD
CD/DE
CA/CE

@m12

Une méthode simple pour écrire les rapports si les angles correspondants sont écrits dans le même ordre.
Pour les triangles : $A C D$ et $D E C$ .
Soit $A C D$
et $D E C$
pour écrire les rapports, je choisis deux lettres du premier triangle et les deux lettres du second triangle qui correspondent.
Soit si je prends les deux premières lettres cela donne : $ACDE\dfrac{AC}{DE}$
Si je prends les deux dernières lettres cela donne : $CDEC\dfrac{CD}{EC}$

Si je prends les deux lettres extrêmes cela donne : $ADDC\dfrac{AD}{DC}$ .

@m12 a dit dans Autre probleme se géométrie 3 eme :

@Noemi a dit dans Autre probleme se géométrie 3 eme :

@m12

Non,

Vérifie les rapports que tu as écrits.

CE/CD
CD/DE
CA/CE

Non
Je pense
AC/CE
DB/CE

@Noemi a dit dans Autre probleme se géométrie 3 eme :

@m12

Une méthode simple pour écrire les rapports si les angles correspondants sont écrits dans le même ordre.
Pour les triangles : $A C D$ et $D E C$ .
Soit $A C D$
et $D E C$
pour écrire les rapports, je choisis deux lettres du premier triangle et les deux lettres du second triangle qui correspondent.
Soit si je prends les deux premières lettres cela donne : $ACDE\dfrac{AC}{DE}$
Si je prends les deux dernières lettres cela donne : $CDEC\dfrac{CD}{EC}$

Si je prends les deux lettres extrêmes cela donne : $ADDC\dfrac{AD}{DC}$ .

Merci méthode génial
Noter dans mon cahier de cours

@Noemi a dit dans Autre probleme se géométrie 3 eme :

@m12

Une méthode simple pour écrire les rapports si les angles correspondants sont écrits dans le même ordre.
Pour les triangles : $A C D$ et $D E C$ .
Soit $A C D$
et $D E C$
pour écrire les rapports, je choisis deux lettres du premier triangle et les deux lettres du second triangle qui correspondent.
Soit si je prends les deux premières lettres cela donne : $ACDE\dfrac{AC}{DE}$
Si je prends les deux dernières lettres cela donne : $CDEC\dfrac{CD}{EC}$

Si je prends les deux lettres extrêmes cela donne : $ADDC\dfrac{AD}{DC}$ .

Dinc CA/DE
CD/EC
AD/DC

@m12

Pas possible avec deux fois $C E$ qui est un côtés non commun à deux triangles.
Il faut bien repérer les angles correspondants égaux.

La dernière réponse est correcte mais il est préférable d'écrire $A C$ plutôt que $C A$ si tu veux appliquer la méthode indiquée.

@Noemi a dit dans Autre probleme se géométrie 3 eme :

@m12

Pas possible avec deux fois $C E$ qui est un côtés non commun à deux triangles.
Il faut bien repérer les angles correspondants égaux.

La dernière réponse est correcte mais il est préférable d'écrire $A C$ plutôt que $C A$ si tu veux appliquer la méthode indiquée.

AC/DE 0.75
Cd/ec 0.78
AD/DE 0.8

@m12 a dit dans Autre probleme se géométrie 3 eme :

@m12 a dit dans Autre probleme se géométrie 3 eme :

@Noemi a dit dans Autre probleme se géométrie 3 eme :

@m12

Non,

Vérifie les rapports que tu as écrits.

CE/CD
CD/DE
CA/CE

Non
Je pense
AC/CE
DB/CE

@Noemi a dit dans Autre probleme se géométrie 3 eme :

@m12

Une méthode simple pour écrire les rapports si les angles correspondants sont écrits dans le même ordre.
Pour les triangles : $A C D$ et $D E C$ .
Soit $A C D$
et $D E C$
pour écrire les rapports, je choisis deux lettres du premier triangle et les deux lettres du second triangle qui correspondent.
Soit si je prends les deux premières lettres cela donne : $ACDE\dfrac{AC}{DE}$
Si je prends les deux dernières lettres cela donne : $CDEC\dfrac{CD}{EC}$

Si je prends les deux lettres extrêmes cela donne : $ADDC\dfrac{AD}{DC}$ .

Merci méthode génial
Noter dans mon cahier de cours

Trop bien votre méthode j ai tout compris
Merci beaucoup

@m12

Parfait si tu as tout compris.