Triangles semblables aide
-
Mm12 dernière édition par
Nouvel exercice
Pouvez vous me corriger
Merci d avanceLes droites AE et CD se coupent EN B
calculer DE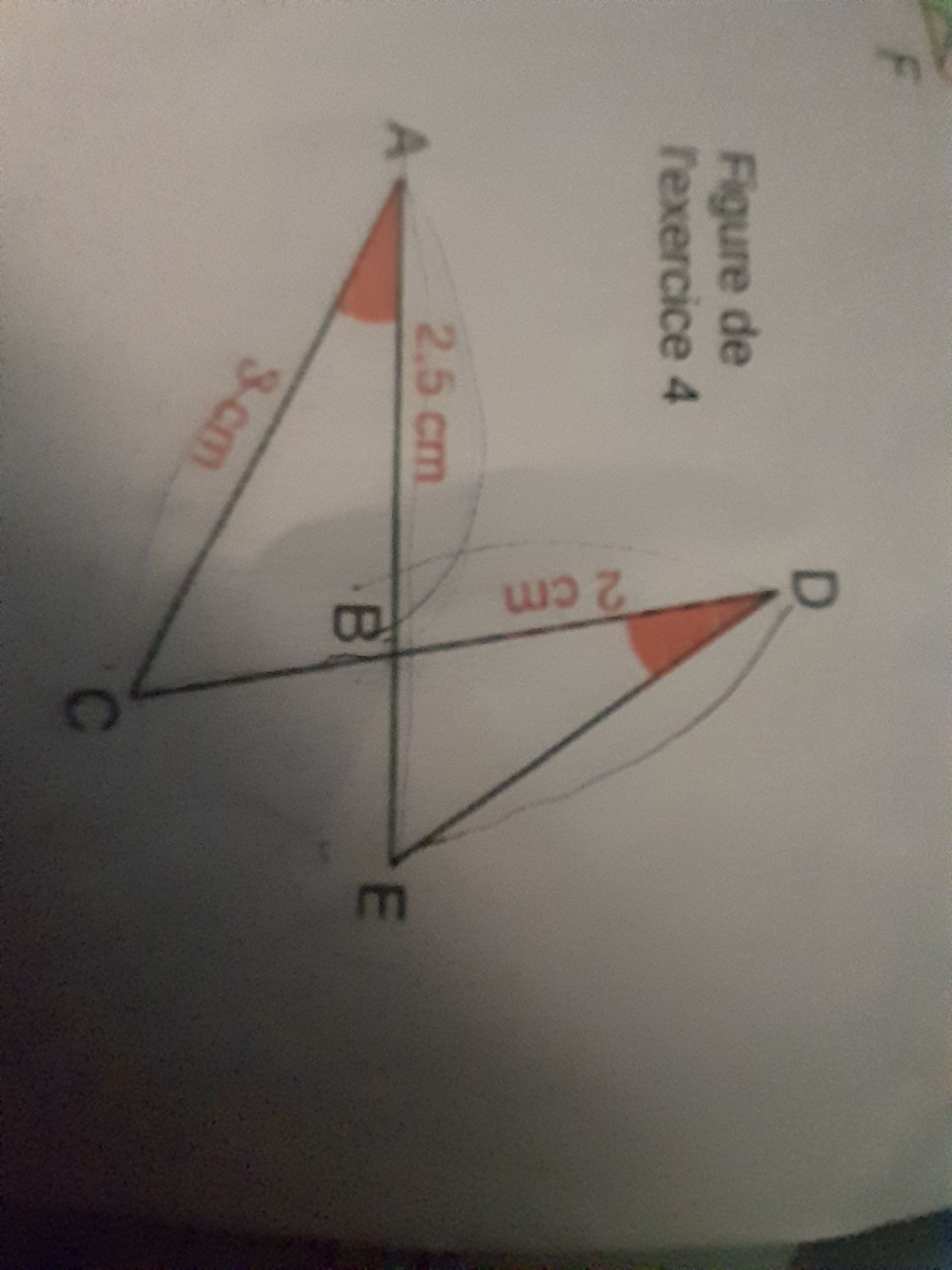
-
Mm12 dernière édition par
@m12 a dit dans Triangles semblables aide :
Nouvel exercice
Pouvez vous me corriger
Merci d avanceLes droites AE et CD se coupent EN B
calculer DE
AC/DE = AB/DB
3/DE = 2.5/2
DE= 3×2/2,5
DE= 2.4 CM
-
@m12 Bonsoir,
Le résultat est correct, mais il faut justifier que les triangles sont semblables.
-
Mm12 dernière édition par
@Noemi a dit dans Triangles semblables aide :
@m12 Bonsoir,
Le résultat est correct, mais il faut justifier que les triangles sont semblables.
Ab/ac= 2.5/3 = 0.8
DB/DE= 2/2.4 = 0.8
-
Mm12 dernière édition par
@m12 a dit dans Triangles semblables aide :
@Noemi a dit dans Triangles semblables aide :
@m12 Bonsoir,
Le résultat est correct, mais il faut justifier que les triangles sont semblables.
Ab/ac= 2.5/3 = 0.8
DB/DE= 2/2.4 = 0.8DE/AC= 2.4/4 = 0.8
-
La justification est à faire avec les angles et non la mesure des côtés car l'énoncé n'indique que trois dimensions.
-
Mm12 dernière édition par
@Noemi a dit dans Triangles semblables aide :
La justification est à faire avec les angles et non la mesure des côtés car l'énoncé n'indique que trois dimensions.
BAC=BDE
-
Il faut indiquer l'égalité pour les trois angles.
Pense aux angles opposés par un même sommet.
-
Mm12 dernière édition par
@Noemi a dit dans Triangles semblables aide :
Il faut indiquer l'égalité pour les trois angles.
Pense aux angles opposés par un même sommet.DCA=DEA
-
Comment tu justifies cette égalité ?
-
Mm12 dernière édition par
@Noemi a dit dans Triangles semblables aide :
Comment tu justifies cette égalité ?
Je sais pas honnêtement help
-
L'énoncé indique : CAB^=BDE^\widehat{CAB}=\widehat{BDE}CAB=BDE
Les angles ABC^\widehat{ABC}ABC et DBE^\widehat{DBE}DBE sont égaux car angles opposés par le sommet BBB.
Les angles ACB^\widehat{ACB}ACB et DEB^\widehat{DEB}DEB sont égaux car la somme des angles d'un triangle est 180°.
Donc les triangles ABCABCABC et BDEBDEBDE sont semblables.On peut donc écrire les rapports égaux.
-
Mm12 dernière édition par
@Noemi a dit dans Triangles semblables aide :
L'énoncé indique : CAB^=BDE^\widehat{CAB}=\widehat{BDE}CAB=BDE
Les angles ABC^\widehat{ABC}ABC et DBE^\widehat{DBE}DBE sont égaux car angles opposés par le sommet BBB.
Les angles ACB^\widehat{ACB}ACB et DEB^\widehat{DEB}DEB sont égaux car la somme des angles d'un triangle est 180°.
Donc les triangles ABCABCABC et BDEBDEBDE sont semblables.On peut donc écrire les rapports égaux.
Merci de votre aide
-
As-tu compris le raisonnement ?
-
Mm12 dernière édition par
@m12 a dit dans Triangles semblables aide :
@Noemi a dit dans Triangles semblables aide :
L'énoncé indique : CAB^=BDE^\widehat{CAB}=\widehat{BDE}CAB=BDE
Les angles ABC^\widehat{ABC}ABC et DBE^\widehat{DBE}DBE sont égaux car angles opposés par le sommet BBB.
Les angles ACB^\widehat{ACB}ACB et DEB^\widehat{DEB}DEB sont égaux car la somme des angles d'un triangle est 180°.
Donc les triangles ABCABCABC et BDEBDEBDE sont semblables.On peut donc écrire les rapports égaux.
Merci de votre aide
Il y a pas une erreur dans la dernière phrase c'est BAC et non ABC ou be me trompe ?
-
Que ce soit le triangle ABCABCABC ou BACBACBAC, c'est le même triangle.
Si tu veux prendre en compte les angles, pour écrire les rapports, tu peux écrire
les triangles ABCABCABC et DBEDBEDBE ou les triangles BACBACBAC et BDEBDEBDE.
-
Mm12 dernière édition par
@Noemi a dit dans Triangles semblables aide :
Que ce soit le triangle ABCABCABC ou BACBACBAC, c'est le même triangle.
Si tu veux prendre en compte les angles, pour écrire les rapports, tu peux écrire
les triangles ABCABCABC et DBEDBEDBE ou les triangles BACBACBAC et BDEBDEBDE.OK j ai compris
Merci