Exercice maths , trouver l'erreur 2nd

Bonjour pouvez vous m'aider svp , j'ai aucune idée de comment faire
tout est dans la photo merci d'avance
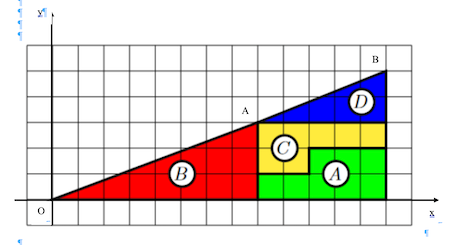
la figure du dessus à celle du dessous on a simplement déplacé les trois figures bc et d aurait on un carré supplémentaire, le carré blanc?
chercher et démontrer d'erreur avec les outils mathématiques de 2nde !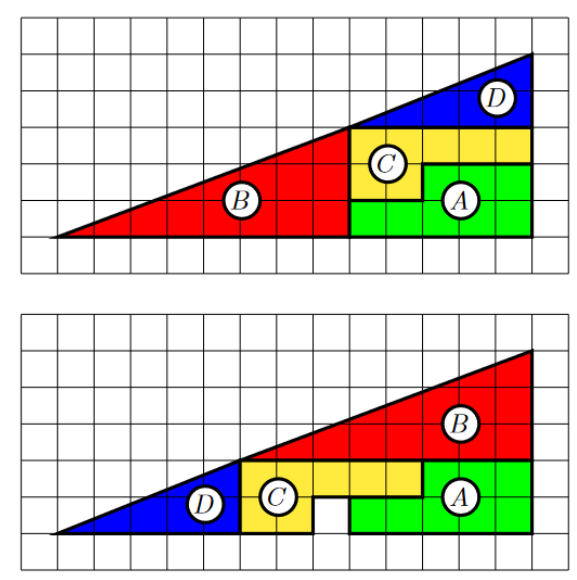 Capture d'écran 2024-03-06 105522.png

@saraaa Bonjour,

Le scan ou un lien de l'énoncé de l'exercice est interdit sur ce forum. Seuls les scans de schémas, graphiques ou figures sont autorisés.
Écris l'énoncé, tes éléments de réponse et indique la question qui te pose problème. Tu obtiendras alors des pistes de résolution.

Le scan va être supprimé par la modération du site.

@Noemi Bonjour , d'accord désolé je ne savais pas

@saraaa

C'est parfait, tu as écris l'énoncé.
Une piste utilise un repère et montre que les points extrêmes des hypoténuses des triangles rectangles ne sont pas sur la même droite.

Je vous avoue que je ne comprend pas trop comment je peut utiliser ca

@saraaa

Dessine un repère sur chaque figure et place des points aux extrémités des hypoténuses.
Exemple : figure du haut : les points $O$ , $A$ et $B$ et sur
la figure du bas , les points $O$ , $C$ et $B$ .
détermine les coordonnées de ces points et analyse la position des points $A$ et $C$ par rapport à la droite $O B$ .

Apres ca je ne sais pas comment l'utilisé ...

@saraaa

Pour la première figure :

@Noemi je n'avais pas compris en vous vouliez en venir , mais je viens de remarquer qu' en fait le triangle du dessus et celui du dessous n'est pas le meme
pour la 1ere figure O(0;0) , A(8:3) B(13;5)
pour celle du dessous O(0;0) C(5;2) et B (13; 5)
On remarque que dans le triangle du dessous l'hypoténuse est légèrement convexe et non dans celui du dessus? si c'est juste comment puis je vraiment écrire ca est ce que c'est bien démontrer? merci

@saraaa

Détermine l'équation de la droite $(O B)$ et montre que les points $A$ et $C$ n'appartiennent pas à cette droite et qu'un point est au dessus et l'autre en dessous.
Puis tu conclus.

l'équation de la droite Ob est 2x+5 , mais A et C appartiennent a cette droite ?

@saraaa

Non, l'équation de la droite $(O B)$ est : $\dfrac{5}{13}x$ .

peut on dire que 2x+5 est la meme chose que 5/13 x?
Parceque c'est plus pratique de savoir si A et C appartiennent a la droite avec ceet equation pour la droite

@saraaa

Non,
$2 x + 5$ n'est pas égal à $513x\dfrac{5}{13}x$
vérification simple en prenant :
$x = 0$ ou $x = 1$
et
avec
$y = 2 x + 5$ , le point $O$ et le point $B$ n'appartiennent pas à cette droite.

@saraaa
Avec le point $A$ de coordonnées $(8; 3)$
$513×8=4013\dfrac{5}{13}\times 8 = \dfrac{40}{13}$ valeur non égale à $3$ mais supérieure à $3$
Avec le point $C$ .....
....

Oui merci je trouve 3,07 pour A donc ce n'est pas= a 3
et 1,92 pour C qui n'est pas égal a 2
donc les 2 points n'appartiennent pas a la droite OB donc les triangles ne sont pas pareille?

@saraaa

La figure globale ne correspond pas à un triangle. Les deux figures sont donc différentes ainsi que leurs aires.

en analysant les deux figures on remarque que les figures ne sont pas semblables et la ligne qui représente l'hypoténuse n'est pas identique en regardant le triangle B on remarque que l'hypoténuse est légèrement converse .
soit A et C les extrémités de l'hypoténuse du triangle B et D A(8;3) C(5;2) l'équation de la droite (ob) est y = 5/ 13 x
On vérifie si A et C appartiennent à ob = 5 / 13 x
5 / 13 x 8 = 3,0 7 qui n'est pas égal à 3
5/13 x 5= 1,92 qui n'est pas égal a 2
donc les points A et C n'appartiennent pas à droite OB la figure ne correspond donc pas à un triangle les figures sont différentes et leurs heure également.
Pouvez vous me dire si c'est juste svp ?merci énormement de votre aide

Bonjour,

Un peu autrement ...

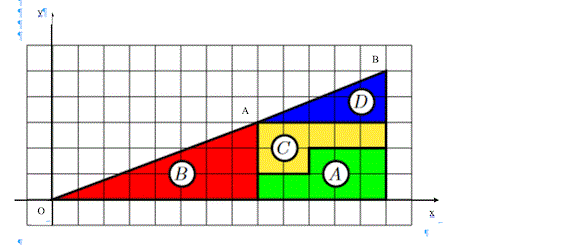
Sans titre.png

Le coefficient directeur de la droite (OA) est m1 = 3/8
Le coefficient directeur de la droite (AB) est m2 = 2/5

m1 est différent de m2 et donc les points O, A et B ne sont pas alignés.

@Black-Jack Bonjour

@saraaa a dit dans Exercice maths , trouver l'erreur 2nd :

en analysant les deux figures on remarque que les figures ne sont pas semblables et la ligne qui représente l'hypoténuse n'est pas identique en regardant le triangle B on remarque que l'hypoténuse est légèrement converse .
soit A et C les extrémités de l'hypoténuse du triangle B et D A(8;3) C(5;2) l'équation de la droite (ob) est y = 5/ 13 x
On vérifie si A et C appartiennent à ob = 5 / 13 x
5 / 13 x 8 = 3,0 7 qui n'est pas égal à 3
5/13 x 5= 1,92 qui n'est pas égal a 2
donc les points A et C n'appartiennent pas à droite OB la figure ne correspond donc pas à un triangle les figures sont différentes et leurs heure également.
Pouvez vous me dire si c'est juste svp ?merci énormement de votre aide

Donc c 'est faut de le faire avec cette équation de droite ou est ce un autre moyen ?

@saraaa a dit dans Exercice maths , trouver l'erreur 2nd :

@Black-Jack Bonjour

@saraaa a dit dans Exercice maths , trouver l'erreur 2nd :

en analysant les deux figures on remarque que les figures ne sont pas semblables et la ligne qui représente l'hypoténuse n'est pas identique en regardant le triangle B on remarque que l'hypoténuse est légèrement converse .
soit A et C les extrémités de l'hypoténuse du triangle B et D A(8;3) C(5;2) l'équation de la droite (ob) est y = 5/ 13 x
On vérifie si A et C appartiennent à ob = 5 / 13 x
5 / 13 x 8 = 3,0 7 qui n'est pas égal à 3
5/13 x 5= 1,92 qui n'est pas égal a 2
donc les points A et C n'appartiennent pas à droite OB la figure ne correspond donc pas à un triangle les figures sont différentes et leurs heure également.
Pouvez vous me dire si c'est juste svp ?merci énormement de votre aide

Donc c 'est faut de le faire avec cette équation de droite ou est ce un autre moyen ?

C'est un autre moyen.

@saraaa

Il est faux d'écrire que pour le triangle B, son hypoténuse est légèrement convexe.
Ce sont les aires des figures qui sont différentes. on peut préciser que l'aire que la deuxième figure est supérieure à celle de la première vu la position des points $A$ et $C$ par rapport à la droite.

d'accord merci , mais pourquoi on ne peut pas dire que l'extremité de l'hypotenuse est convexe ? ca semble etre le cas ?

@saraaa

Si c'est une hypoténuse, le triangle serait rectangle. est-ce le cas ?