Fonctions exponentielle

Bonsoir
Pour tout entier n ≥ 1, on considère la fonction de la variable réelle , $f_{n}(x)=x^ne^(-x)$
Donner le domaine de définition de fn, et calculer sa dérivée.
Df= R je pense mais je ne sais pas pourquoi, est-ce un polynôme?
$f_{n}^’(x)=(n-x)x^{n-1}e^{-x}$
(b) Montrer que toutes les courbes représentatives de fn ont deux points communs, que l’on déterminera.
Aidez moi svp avc la question b

@Zeïnab-Mahamadou Bonjour,

Résous l'équation $f_n(x)= f_{n+1}(x)$

@Noemi pourquoi tirer quoi

@Noemi j’ai transformé ça en $x^{2n+1})e^{-x}$ =0 ca peu marché?

@Zeïnab-Mahamadou

$x^{n+1}e^{-x}=x^ne^{-x}$
$x^{n+1}e^{-x}-x^ne^{-x}=0$
En factorisant :
$x^ne^{-x}(x-1)=0$
donc les solutions pour $x$ sont ....

@Noemi X=1 et l’autre le n me bloque

@Zeïnab-Mahamadou

$x^n= 0$ si $x = 0$ .

Détermine l'ordonnée de chaque points.

@Noemi bonsoir j’ai pas compris

@Zeïnab-Mahamadou

Tu n'as pas compris quoi ?

@Noemi bonsoir
x^n=0 si x=0

Les cordonnees seront (0;0)?

@Zeïnab-Mahamadou

Un produit est nul si et seulement si l'un des facteurs est nul.
$x×x×x.......×x=0x\times x\times x .......\times x= 0$ donne $x = 0$

Si $x = 0$ ; $f_n(0)=0^ne^{-0}=0$ .
Donc le premier point est le point $O (0; 0)$

Même raisonnement pour $x = 1$ .

@Noemi d’accord merci beaucoup

Bonjour,

Illustration graphique avec quelques valeurs de $n$

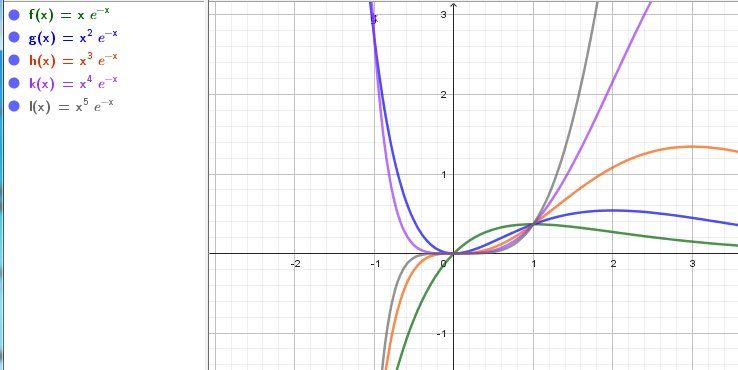
Remarque ,
Il était possible, pour trouver les points communs, de commencer par prendre, par exemple, $n = 1$ et $n = 2$ et de résoudre le système :
${y=xe−xy=x2e−x\begin{cases} y=xe^{-x}\cr y=x^2e^{-x}\end{cases}$

On trouve ainsi les couples $(x, y)$ solutions : $0,0), (1,e^{-1})$

Ensuite on vérifie que ces couples sont satisfaisants pour tout $n$ de $N^*$ car :
$f_n(0)=0$ et $f_n(1)=e^{-1}$