étude de fonction cos(π ℯ^(x))
-
Gguillaume M dernière édition par
Bonjour, on me demande d'étudier la fonction entre l'intervalle -6 à 1
f(x)=cos(π ℯ^(x))
J'en est déduis que la fonction était ni paire ni impaire
que la fonction s'annule en x=ln((1/2)+k)
la dérivée première donne:
f'(x)= -sin(π ℯ^(x)) *π ℯ^(x)
et la dérivée première s'annule (d'abord enlever le (-) et le π):
ℯ^(x) donne -infini donc pas de zéro et pour l'autre j'obtiens x=ln(k)
et je suis bloqué là j'ai mis dans le tableau que quand k=1 car les autres je connais pas la valeur et plus petit ou égale à 0 on peut pas. je sais plus quoi faire avec ça
-
@guillaume-M Bonjour,
Tu fais varier kkk jusqu'a ce que xxx soit supérieur à 1.
donc si k=2k= 2k=2; ln(2)=....ln(2) = ....ln(2)=.... donc la valeur de xxx est possible.
Si k=3k= 3k=3 ; ln(3)=....ln(3) = ....ln(3)=.... donc ....
-
Gguillaume M dernière édition par
Mercii j'ai compris et dans une étude de fonction je dois encore allez plus loin à part faire le graphique et la dérivée seconde qu'on me demande pas ?
-
Pour l'étude d'une fonction, les différentes étapes :
le domaine de définition ;
la parité ou la périodicité,
les limites aux bornes du domaine de définition pour déterminer les éventuelles asymptotes.
la dérivée
le tableau de variations
éventuellement la dérivée seconde
la représentation graphique
-
mtschoon dernière édition par mtschoon

Bonjour,
@guillaume-M , tu as dû te tromper de rubrique car ta question ne correspond pas au programme français de 6ème/5ème
Peut-être es tu en Belgique ?...
La modération déplacera certainement ton topic.Pour te faire une idée du problème et du travail à accomplir je te conseille de faire la courbe ave ta calculatrice.
Cela t'éclairera.
Si besoin, je te joins un schéma :
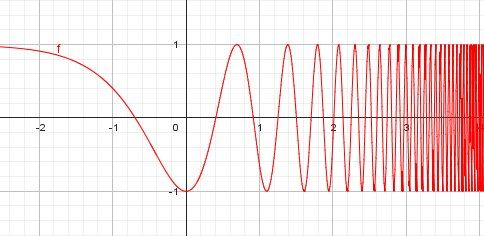
-
Gguillaume M dernière édition par
@mtschoon mes sincères excuse j'ai dû le tromper et je n'ai pas une calculatrice qui fait des courbes

-
mtschoon dernière édition par

Pas de soucis @guillaume-M .
La modération vient de déplacer ton Topic.