4 points coplanaires

Rebonjour,

je publie un autre exercice sur lequel je bloque (en fait exactement sur le même point que le post précédent).

ENONCE

ABCD un tétraèdre.
I,J,K,L milieux respectifs de [AB], [AC], [CD], [BD].

I,J,K,L sont ils coplanaires ? (méthode sans repère)
idem avec repère
$- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -$

Pas de difficulté avec la méthode utilisant un repère.
Comme il existe 2 réels $α\alpha$ et $β\beta$ tels que $IJ→=αIL→+βIK→\overrightarrow{IJ}=\alpha \overrightarrow{IL}+\beta \overrightarrow{IK}$ alors I,J, K et L sont coplanaires.

Mais sans utiliser de repère je n'y parviens pas.
Je trouve bien des rapports entre vecteurs en utilisant le théorème des droites de milieux mais je n'arrive pas à conclure ... grrrr

Pourriez-vous m'indiquer un petit indice ?

Merci par avance pour votre aide !

PS : un petit schéma pour vous aider à vous repérer

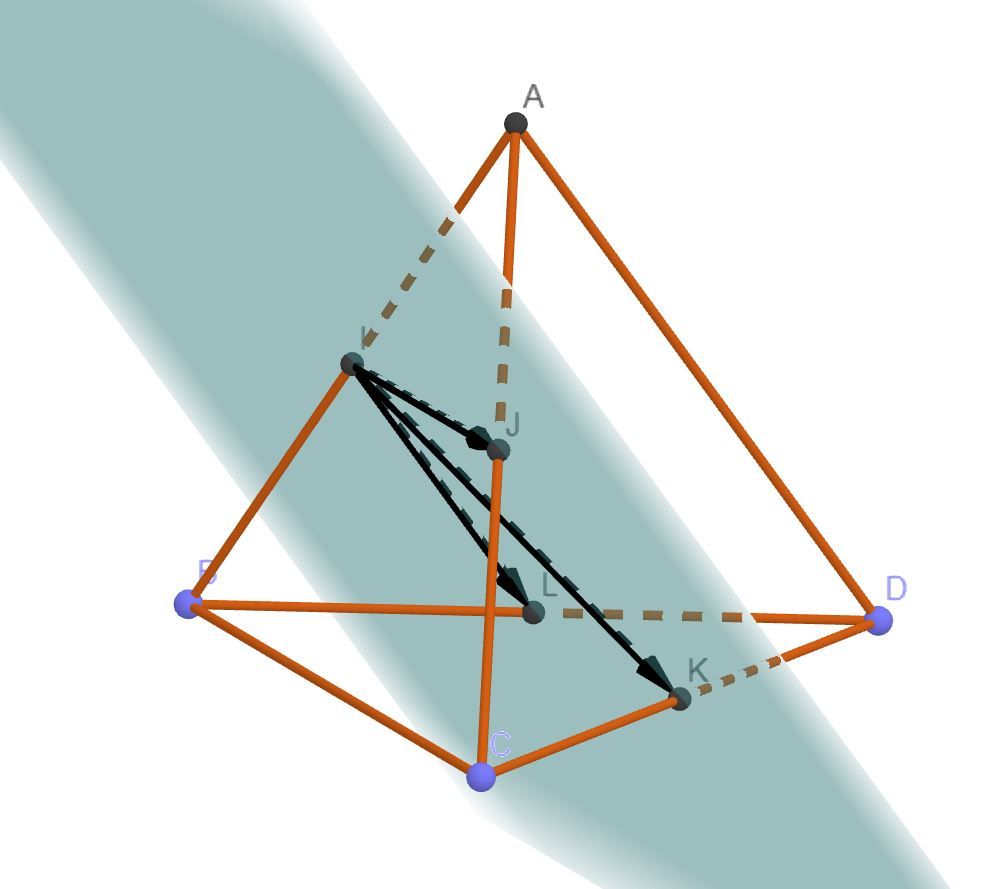
@Chris21300 Bonjour,

Compare les vecteurs $IJ→\overrightarrow{IJ}$ et $LK→\overrightarrow{LK}$ .

Merci @Noemi ,

$IJ→=12BC→\overrightarrow{IJ}= \frac {1}{2}\overrightarrow{BC}$ (droite des milieux)
$LK→=12BC→\overrightarrow{LK}= \frac {1}{2}\overrightarrow{BC}$ (droite des milieux)

d'où $IJ→=LK→\overrightarrow{IJ}= \overrightarrow{LK}$ (droite des milieux)

Par contre je ne vois pas où aller

@Chris21300

Relation de Chasles : $IL→=IJ→+JK→+KL→\overrightarrow{IL}= \overrightarrow{IJ}+\overrightarrow{JK}+\overrightarrow{KL}$ .

heu ... Oui je connais la relation de Chasles ... Mais désolé @Noemi je ne comprends pas le rapport avec la question posée
Je ne doute pas que ta réponse soit la bonne, mais je la comprends pas

@Chris21300

Simplifie la relation, en utilisant ton résultat précédent.

@Noemi

On obtient $IL→=JK→\overrightarrow{IL}=\overrightarrow{JK}$ .... Mais ... Je tourne en rond

@Chris21300

Si $IL→=JK→\overrightarrow{IL}=\overrightarrow{JK}$ alors le quadrilatère $I L K J$ est un parallélogramme, donc ...

@Noemi

arf ...du coup I,J,K, L sont coplanaires !

Je cherchais désespérément à obtenir $IJ→=αIK→+βIL→\overrightarrow{IJ}=\alpha\overrightarrow{IK}+\beta\overrightarrow{IL}$ pour conclure

Quand on est obnubilté par une idée on ne voit pas les évidence a proximité ...effet tunnel !!!

Encore merci @Noemi

@Noemi ,

Mais alors, du coup, quand j'ai écrit :

$IJ→=12BC→\overrightarrow{IJ}= \frac {1}{2}\overrightarrow{BC}$ (droite des milieux)
$LK→=12BC→\overrightarrow{LK}= \frac {1}{2}\overrightarrow{BC}$ (droite des milieux)

d'où $IJ→=LK→\overrightarrow{IJ}= \overrightarrow{LK}$ (droite des milieux)

Il me suffisait d'en déduire que IJKL était un parallélogramme et donc que I,J,K et L étaient coplanaires ?

@Chris21300

Oui