Résoudre une équation
-
Qqi98 dernière édition par qi98
Bonjour à tous,
A 71 ans pour ne pas rester en berne avec ma petite fille, et pour moi-même pour mon site, je désirais me remette aux équations que je n'aie pas pratiquées depuis plus de 50 ans.
Je sais, ou crois savoir, que les méthodes d'enseignement ont bien changé depuis, mais je pense que le résultat est le même.
−3(2x)2+16x−32=-3(2x)^2+16x-32=−3(2x)2+16x−32=
Ca ne doit pas être compliqué mais j'ai un trou, un ravin même, concernant −3(2x)2-3(2x)^2−3(2x)2. Là, je ne me souviens plus !
Pour bien faire, il faudrait décomposer la 1ère opération je crois :
(2x)(2x) et je ne sais plus comment faire, en plus, il y a le -3 qui me pose problème !Merci d'avance de votre aide.
-
Ffustel dernière édition par
@qi98
Bonjour.
Tout d'abord j'espère que l'équation doit être égale à 0.
Il faut développer -3(2x)^2 ce qui fait -12x^2.
Puis appliquer le déterminant et résoudre l'équation
-
Ffustel dernière édition par
@fustel
Vous pourriez aussi simplifier l'équation finale. J'insiste sur le fait que l'équation doit être égale à 0
-
Ffustel dernière édition par
Au final, l'équation sera: -3x^2+4x-8=0.après simplification
Le déterminant est égal à b^2-4ac donc le déterminant est égal à -80.
Comme le déterminant est négatif, l'équation est impossible
-
Qqi98 dernière édition par qi98
@fustel a dit dans Résoudre une équation :
Comme le déterminant est négatif, l'équation est impossibleBonjour, oui je sais, on en parle beaucoup sur internet.
Donc, il me faudrait changer certains ou mettre une autre équation après "=" ?
-
Qqi98 dernière édition par qi98
@fustel a dit dans Résoudre une équation :
@fustel
Vous pourriez aussi simplifier l'équation finale. J'insiste sur le fait que l'équation doit être égale à 0Admettons que ça soit 0, votre réponse ne m'apprend rien !
Donc, pour faire plus simple, je mettrais une autre équation.
-
@qi98 Bonjour,
Oui, proposez une équation avec un nouveau sujet.
-
Qqi98 dernière édition par
@fustel a dit dans Résoudre une équation :
Le déterminant est égal à b^2-4ac donc le déterminant est égal à -80.
Comme le déterminant est négatif, l'équation est impossibleDésolé de mes oublis ! Ca fait plus de 50 ans tout de même !
Franchement, je suis perdu entre déterminant positif ou négatif.
D'abord, c'est quoi exactement le déterminant ?
-
mtschoon dernière édition par mtschoon

Bonjour,
Je ne fais que passer car trop d'activités en ce moment.
@qi98 a dit dans Résoudre une équation :
@fustel a dit dans Résoudre une équation :
Le déterminant est égal à b^2-4ac donc le déterminant est égal à -80.
Comme le déterminant est négatif, l'équation est impossibleDésolé de mes oublis ! Ca fait plus de 50 ans tout de même !
Franchement, je suis perdu entre déterminant positif ou négatif.
D'abord, c'est quoi exactement le déterminant ?Pour la résolution d'une équation du second degré de la forme ax2+bx+c=0ax^2+bx+c=0ax2+bx+c=0 avec a≠0a\ne0a=0 , il ne s'agit pas de "déterminant" mais du "DISCRIMINANT" de l'équation.
De façon usuelle, ce discriminant se note Δ\DeltaΔ
Δ=b2−4ac\Delta=b^2-4acΔ=b2−4acRegarde la partie II du cours ici :
https://www.mathforu.com/premiere-s/le-second-degre-1ere-partie/
-
BBlack-Jack dernière édition par
Bonjour,
−3(2x)2+16x−32=0-3(2x)^2 + 16x - 32 = 0−3(2x)2+16x−32=0
−3(4x2)+16x−32=0-3(4x^2) + 16x - 32 = 0−3(4x2)+16x−32=0
−12x2+16x−32=0-12x^2 + 16x - 32 = 0−12x2+16x−32=0Alternative ... si l'élève n'a pas encore appris la méthode avec de DISCRIMINANT :
On peut, par exemple, passer par la forme canonique ...
En détail :−12(x2−1612x+3212)=0-12(x^2 - \frac{16}{12}x + \frac{32}{12}) = 0−12(x2−1216x+1232)=0
−12(x2−43x+83)=0-12(x^2 - \frac{4}{3}x + \frac{8}{3}) = 0−12(x2−34x+38)=0On multiplie les 2 membres par -1/12 et on obtient :
x2−43x+83=0x^2 - \frac{4}{3}x + \frac{8}{3} = 0x2−34x+38=0Se rappeler que (a-b)² = a²-2ab-b² et il vient :
(x−23)2−49+83=0(x - \frac{2}{3})^2 - \frac{4}{9} + \frac{8}{3} = 0(x−32)2−94+38=0
(x−23)2−49+249=0(x - \frac{2}{3})^2 - \frac{4}{9} + \frac{24}{9} = 0(x−32)2−94+924=0
(x−23)2+209=0(x - \frac{2}{3})^2 + \frac{20}{9} = 0(x−32)2+920=0Comme (x−23)2(x - \frac{2}{3})^2(x−32)2 > 000 et que 209\frac{20}{9}920 > 000, l'équation n'a pas de solution car la somme de 2 quantités strictement positives ne peut pas être nulle.
-
Qqi98 dernière édition par qi98
@mtschoon a dit dans Résoudre une équation :
Bonjour,
Je ne fais que passer car trop d'activités en ce moment.
@qi98 a dit dans Résoudre une équation :
@fustel a dit dans Résoudre une équation :
Le déterminant est égal à b^2-4ac donc le déterminant est égal à -80.
Comme le déterminant est négatif, l'équation est impossibleDésolé de mes oublis ! Ca fait plus de 50 ans tout de même !
Franchement, je suis perdu entre déterminant positif ou négatif.
D'abord, c'est quoi exactement le déterminant ?Pour la résolution d'une équation du second degré de la forme ax2+bx+c=0ax^2+bx+c=0ax2+bx+c=0 avec a≠0a\ne0a=0 , il ne s'agit pas de "déterminant" mais du "DISCRIMINANT" de l'équation.
De façon usuelle, ce discriminant se note Δ\DeltaΔ
Δ=b2−4ac\Delta=b^2-4acΔ=b2−4acRegarde la partie II du cours ici :
https://www.mathforu.com/premiere-s/le-second-degre-1ere-partie/Bonjour,
Désolé mais j'ai plus l'habitude d'entendre parler de "déterminant" que "discriminent" ! En plus, ça ne me dit strictement plus rien ce "Δ" !Et merci pour le lien, mais tous ceux, et il y en a beaucoup, expliquent pratiquement la même chose, et ça ne m'avance guère, j'aurais même tendance à dire que ça s'embrouille dans mon esprit parce que chacun explique à sa manière !
Mais merci de vouloir m'aider.
-
Qqi98 dernière édition par qi98
@Black-Jack a dit dans Résoudre une équation :
Bonjour,
−3(2x)2+16x−32=0-3(2x)^2 + 16x - 32 = 0−3(2x)2+16x−32=0
−3(4x2)+16x−32=0-3(4x^2) + 16x - 32 = 0−3(4x2)+16x−32=0
−12x2+16x−32=0-12x^2 + 16x - 32 = 0−12x2+16x−32=0Alternative ... si l'élève n'a pas encore appris la méthode avec de DISCRIMINANT :
On peut, par exemple, passer par la forme canonique ...
En détail :−12(x2−1612x+3212)=0-12(x^2 - \frac{16}{12}x + \frac{32}{12}) = 0−12(x2−1216x+1232)=0
−12(x2−43x+83)=0-12(x^2 - \frac{4}{3}x + \frac{8}{3}) = 0−12(x2−34x+38)=0On multiplie les 2 membres par -1/12 et on obtient :
x2−43x+83=0x^2 - \frac{4}{3}x + \frac{8}{3} = 0x2−34x+38=0Se rappeler que (a-b)² = a²-2ab-b² et il vient :
(x−23)2−49+83=0(x - \frac{2}{3})^2 - \frac{4}{9} + \frac{8}{3} = 0(x−32)2−94+38=0
(x−23)2−49+249=0(x - \frac{2}{3})^2 - \frac{4}{9} + \frac{24}{9} = 0(x−32)2−94+924=0
(x−23)2+209=0(x - \frac{2}{3})^2 + \frac{20}{9} = 0(x−32)2+920=0Comme (x−23)2(x - \frac{2}{3})^2(x−32)2 > 000 et que 209\frac{20}{9}920 > 000, l'équation n'a pas de solution car la somme de 2 quantités strictement positives ne peut pas être nulle.
Bonjour et merci de votre réponse.
Personnellement, je ne me souviens pas du tout de ce "discriminent" dont tout le monde parle et je ne sais pas si on en parlait il y a + de 50 ans, en tout cas pour moi, ça ne me dit rien, encore moins "canonique" ! .
Mais je suppose, je dis bien "je suppose" qu'elle connaît ou pas ces termes.En fait, ce que j'ai mis n'est pas juste puisque vous me dites qu'il n'y a pas de solution !
J'ai donc choisi les mauvais nombres !Alors j'ai enlevé le "32".
Ce qui me donnerait :
3−(2x)²+16x=03-(2x)²+16x=03−(2x)²+16x=0
3−(2x)(2x)+16x=03-(2x)(2x)+16x=03−(2x)(2x)+16x=0
−(2x)(2x)+16x=−3-(2x)(2x)+16x=-3−(2x)(2x)+16x=−3
12x=−312x=-312x=−3
x=−3/12=−1/4=−0,25x=-3/12=-1/4=-0,25x=−3/12=−1/4=−0,25
Désolé mais je n'arrive à mettre sous forme de fraction comme vous l'avez fait, je n'arrive pas à savoir comment vous arrivez à faire ça.
J'ai .bien "12\dfrac{1}{2}21" mais je n'arrive pas à le placer correctement :
-
@qi98 Bonjour,
Attention
3−(2x)2+16x=03-(2x)^2+16x=03−(2x)2+16x=0 donne
3−4x2+16x=03-4x^2+16x=03−4x2+16x=0 soit
−4x2+16x+3=0-4x^2+16x+3=0−4x2+16x+3=0 ou
4x2−16x−3=04x^2-16x-3=04x2−16x−3=0
(2x−4)2−16−3=0(2x-4)^2-16-3=0(2x−4)2−16−3=0
(2x−4)2−19=0(2x-4)^2-19=0(2x−4)2−19=0
Il faut ensuite utiliser l'identité remarquable a2−b2=(a−b)(a+b)a^2-b^2=(a-b)(a+b)a2−b2=(a−b)(a+b)
-
Qqi98 dernière édition par qi98
@Noemi a dit dans Résoudre une équation :
@qi98 Bonjour,
Attention
3−(2x)2+16x=03-(2x)^2+16x=03−(2x)2+16x=0 donne
3−4x2+16x=03-4x^2+16x=03−4x2+16x=0 soit
−4x2+16x+3=0-4x^2+16x+3=0−4x2+16x+3=0 ou
4x2−16x−3=04x^2-16x-3=04x2−16x−3=0
(2x−4)2−16−3=0(2x-4)^2-16-3=0(2x−4)2−16−3=0
(2x−4)2−19=0(2x-4)^2-19=0(2x−4)2−19=0
Il faut ensuite utiliser l'identité remarquable a2−b2=(a−b)(a+b)a^2-b^2=(a-b)(a+b)a2−b2=(a−b)(a+b)Bonjour Noemi,
Je vois que j'ai tout faux ???
Quant à l'identité remarquable que vous mettez, alors là, je suis complètement perdu.
Je ne vois comment transposer l'équation en IR !
Voulez-vous m'expliquer ?Je suis perdu entre les IR, les changements de signe si on enlève les parenthèses et certaines choses encore !
Moi, je vois ça comme ça, et c'est peut-être pas bon :
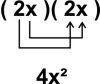 Je vois que les 4x²4x²4x² que vous avez mis ça pourrait fait comme ça ?
Je vois que les 4x²4x²4x² que vous avez mis ça pourrait fait comme ça ?Comme je ne suis pas à l'aise avec les IR, j'aurais calculé −4x²+16x+3=0-4x² + 16x + 3 = 0−4x²+16x+3=0 en faisant −4x²+16X=3-4x² + 16X = 3−4x²+16X=3 et encore, parce que je ne vois pas comment faire pour −4x²+16x-4x² + 16x−4x²+16x ???
Alors si j'ai (−4x²−16x)(-4x² - 16x)(−4x²−16x) je ferais 4x+16x4x + 16x4x+16x, ou alors c'est pire que ce que je pensais, je mélange tout.
-
(2x−4)2−19=0(2x-4)^2-19=0(2x−4)2−19=0
(2x−4)2−(19)2=0(2x-4)^2-(\sqrt19)^2=0(2x−4)2−(19)2=0
Il faut ensuite utiliser l'identité remarquable a2−b2=(a−b)(a+b)a^2-b^2=(a-b)(a+b)a2−b2=(a−b)(a+b)
avec a=2x−4a=2x-4a=2x−4 et b=19b= \sqrt{19}b=19
L'équation devient :
(2x−4−19)(2x−4+19)=0(2x-4-\sqrt{19})(2x-4+\sqrt{19})=0(2x−4−19)(2x−4+19)=0
et un produit de facteurs est nul si et seulement si l'un de ses facteurs est nul.
donc il reste à résoudre :
2x−4−19=02x-4-\sqrt{19}=02x−4−19=0 et
2x−4+19=02x-4+\sqrt{19}=02x−4+19=0
-
Qqi98 dernière édition par
@Noemi a dit dans Résoudre une équation :
(2x−4)2−19=0(2x-4)^2-19=0(2x−4)2−19=0
(2x−4)2−(19)2=0(2x-4)^2-(\sqrt19)^2=0(2x−4)2−(19)2=0
Il faut ensuite utiliser l'identité remarquable a2−b2=(a−b)(a+b)a^2-b^2=(a-b)(a+b)a2−b2=(a−b)(a+b)
avec a=2x−4a=2x-4a=2x−4 et b=19b= \sqrt{19}b=19
L'équation devient :
(2x−4−19)(2x−4+19)=0(2x-4-\sqrt{19})(2x-4+\sqrt{19})=0(2x−4−19)(2x−4+19)=0
et un produit de facteurs est nul si et seulement si l'un de ses facteurs est nul.
donc il reste à résoudre :
2x−4−19=02x-4-\sqrt{19}=02x−4−19=0 et
2x−4+19=02x-4+\sqrt{19}=02x−4+19=0Bonjour Noemi,
Effectivement, ça n'a l'air compliqué, mais je ne me souviens pas du tout cette histoire de comparer certaines équations avec les IR ????
Comme vous le montrez c'est simple, mais j'ai encore du mal à comprendre cette histoire de facteur nul ou pas ????
Donc, si le comprends bien cela serait "S { x ; y }" par exemple !
Si c'est ça, autant que j'abandonne de suite !J'ai un vague souvenir des signes qui changent si on enlève les parenthèses, et encore, ou qui passent de l'autre côté du signe égal, et encore je me trompe peut-être !
-
2x−4−19=02x-4-\sqrt{19}=02x−4−19=0 donnę 2x=4+192x=4+\sqrt{19}2x=4+19, soit x=4+192x= \dfrac{4+\sqrt{19}}{2}x=24+19
2x−4+19=02x-4+\sqrt{19}=02x−4+19=0 donnę 2x=4−192x=4-\sqrt{19}2x=4−19, soit x=4−192x= \dfrac{4-\sqrt{19}}{2}x=24−19La solution de l'équation est : S={4−192;4+192}S=\lbrace \dfrac{4-\sqrt{19}}{2} ; \dfrac{4+\sqrt{19}}{2}\rbrace S={24−19;24+19}
-
Qqi98 dernière édition par
@Noemi a dit dans Résoudre une équation :
2x−4−19=02x-4-\sqrt{19}=02x−4−19=0 donnę 2x=4+192x=4+\sqrt{19}2x=4+19, soit x=4+192x= \dfrac{4+\sqrt{19}}{2}x=24+19
2x−4+19=02x-4+\sqrt{19}=02x−4+19=0 donnę 2x=4−192x=4-\sqrt{19}2x=4−19, soit x=4−192x= \dfrac{4-\sqrt{19}}{2}x=24−19La solution de l'équation est : S={4−192;4+192}S=\lbrace \dfrac{4-\sqrt{19}}{2} ; \dfrac{4+\sqrt{19}}{2}\rbrace S={24−19;24+19}
Je m'en doutais un peu avec vos explications.
Voyez-vous, j'ai 71 ans maintenant et ma dernière classe était la 5ème et une demi 4ème, ensuite, je me suis engagé dans le Marine Nationale.
Je sais que les méthodes d'enseignement ont changé pour aboutir aux mêmes résultats, mais j'ai pratiquement tout oublié et malgré vos explications, qui sont simples pour vous, font que je m'y perds parce chacune et chacun, pas spécialement ici, donne sa solution pour le même résultat.
Je pensais que ça reviendrait vite, mais je me suis trompé.
Donc, je pense que je vais m'arrêter là car j'ai perdu une partie de mes neurones qui m'auraient servies, et comme il n'y a pas de neurones en promo à Auchan, c'est vite calculé.Merci de m'avoir aidé mais je n'ai plus de courage pour trouver une solution.