Inégalité de Bienaymé-Tchebychev

Bonjour tout le monde,

J'ai un exercice sur les proba (Loi Binomial, inégalité de Bienaymé-Tchebychev). Et je bloque totalement sur une question, le reste j'ai pu le résoudre. Je vous écris ci-dessus le sujet, en donnant les données les plus importantes et la question :

Une compagnie aérienne exploite un avion d'une capacité de 200 places, on admet que la probabilité qu'un passagers ayant réservé son billet se présente est de p= 0,8

La compagnie souhaite vendre n billets avec n > 200, en limitant à 5 % le risque que plus de 200 personnes se présentent.

On suppose que np > 200

On simule la situation, la compagnie a vendu un billet avec 200 < n < 250

On définit la variable aléatoire Sn, le nombre de personnes, parmi les n personnes se présentant à l'embarquement.

J'ai donc trouvé que c'était une loi binomial B(n ; 0,8)

Et la relation suivante :

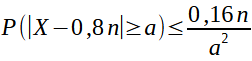
Et la question qui me pose problème est la suivante:

Montrer que :

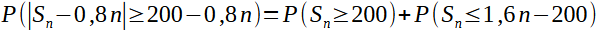
En déduire :

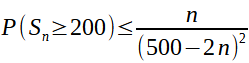
J'ai relu tous mes cours et je n'ai rien trouvé qui puisse m'aider.

Merci d'avance pour votre aide et pour votre temps.
Bonne journée.

@SilenceCurse Bonjour,

Pour l'égalité avec les probabilités, isole $S_n$ de $∣Sn−0,8n∣≥200−0,8n\vert S_n-0,8n\vert \geq 200-0,8n$
puis pour l'inégalité utilise la relation proposée et tu divises numérateur et dénominateur par $0, 16$ .

Bonjour @Noemi, merci beaucoup pour ton aide
Pour l'égalité des proba j'ai donc trouvé :

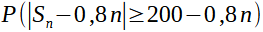
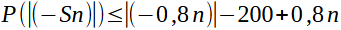
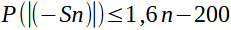
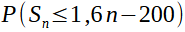
Et

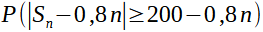
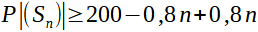
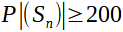
Donc : .

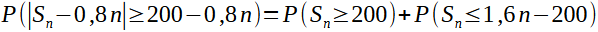Et pour l'inégalité en divisant par 0,16 j'ai trouvé deux résultats différents :

.

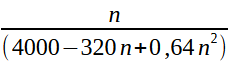
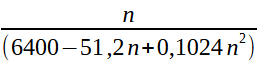Mais je suis absolument sur des résultats.

Merci d'avance pour ton aide.
Bonne journée.

@SilenceCurse

Pour la division par 0,16, vu que le dénominateur est au carré, il faut écrire :
$0,16=0,4^2$
le dénominateur devient
$(200−0,8n0,4)2=(500−2n)2(\dfrac{200-0,8n}{0,4})^2=(500-2n)^2$

Désolé, mais pour arriver l'inégalité voulue, c'est quelles données qu'il faut utiliser, enfin du moins divisier par 0,16

@SilenceCurse

A partir de la relation que tu as démontrée. Tu écris l'inégalité :
$P(Sn≥200)≤P(∣Sn−0,8n∣≥200−0,8n)P(S_n \geq 200) \leq P(\vert S_n -0,8n \vert \geq 200-0,8n)$
puis tu utilises la relation trouvée précédemment
$P(∣Sn−0,8n∣≥200−0,8n)≤0,16n(200−0,8n)2P(\vert S_n -0,8n \vert \geq 200-0,8n)\leq \dfrac{0,16n}{(200-0,8n)^2}$

Il reste à diviser numérateur et dénominateur par $0, 16$ pour trouver l'expression écrite.

Merci infiniment pour l'aide, j'ai enfin compris.

Passe une bonne journée.

@SilenceCurse

C'est parfait si tu as compris.