Exercice suite numériques
-
Mm12 dernière édition par
J en ai encore un
La suite U.n =2n-40n-20
- calculer pour tout entier naturel n; Un+1 ; Un grand + grand 1 et U 2n
-
Mm12 dernière édition par
@m12 a dit dans Exercice suite numériques :
J en ai encore un
La suite U.n =2n-40n-20
- calculer pour tout entier naturel n; Un+1 ; Un grand + grand 1 et U 2n
Pour Un+1= 2n+1-40(n+1)-20 =2n+1-40n-40-20= 2n+1-40n-60
Pour Un grand +grand1 = 2n-40n-20+1 = 2n-40n-19
Pour U2n = 2 2n-40(2n)-20=4n-80n-20
-
@m12 Bonjour,
Je suppose que c'est Un=2n−40n−20U_n= 2^n-40n-20Un=2n−40n−20 ?
Attention aux parenthèses :
Un+1=2(n+1)−40(n+1)−20=....U_{n+1}= 2^{(n+1)}-40(n+1)-20 =....Un+1=2(n+1)−40(n+1)−20=....A quoi correspond UnU_nUn grand ?
Un+1=2n−40n−20+1=...U_n+1=2^n-40n-20 +1= ...Un+1=2n−40n−20+1=...
U2n=22n−40×2n−20=....U_{2n}= 2^{2n}-40\times 2n -20= ....U2n=22n−40×2n−20=....
-
Mm12 dernière édition par
@Noemi a dit dans Exercice suite numériques :
@m12 Bonjour,
Je suppose que c'est Un=2n−40n−20U_n= 2^n-40n-20Un=2n−40n−20 ?
Attention aux parenthèses :
Un+1=2(n+1)−40(n+1)−20=....U_{n+1}= 2^{(n+1)}-40(n+1)-20 =....Un+1=2(n+1)−40(n+1)−20=....A quoi correspond UnU_nUn grand ?
Un+1=2n−40n−20+1=...U_n+1=2^n-40n-20 +1= ...Un+1=2n−40n−20+1=...
U2n=22n−40×2n−20=....U_{2n}= 2^{2n}-40\times 2n -20= ....U2n=22n−40×2n−20=....@Noemi a dit dans Exercice suite numériques :
@m12 Bonjour,
Je suppose que c'est Un=2n−40n−20U_n= 2^n-40n-20Un=2n−40n−20 ?
Attention aux parenthèses :
Un+1=2(n+1)−40(n+1)−20=....U_{n+1}= 2^{(n+1)}-40(n+1)-20 =....Un+1=2(n+1)−40(n+1)−20=....A quoi correspond UnU_nUn grand ?
Un+1=2n−40n−20+1=...U_n+1=2^n-40n-20 +1= ...Un+1=2n−40n−20+1=...
U2n=22n−40×2n−20=....U_{2n}= 2^{2n}-40\times 2n -20= ....U2n=22n−40×2n−20=....
-
Mm12 dernière édition par
@Noemi a dit dans Exercice suite numériques :
@m12 Bonjour,
Je suppose que c'est Un=2n−40n−20U_n= 2^n-40n-20Un=2n−40n−20 ?
Attention aux parenthèses :
Un+1=2(n+1)−40(n+1)−20=....U_{n+1}= 2^{(n+1)}-40(n+1)-20 =....Un+1=2(n+1)−40(n+1)−20=....A quoi correspond UnU_nUn grand ?
Un+1=2n−40n−20+1=...U_n+1=2^n-40n-20 +1= ...Un+1=2n−40n−20+1=...
U2n=22n−40×2n−20=....U_{2n}= 2^{2n}-40\times 2n -20= ....U2n=22n−40×2n−20=....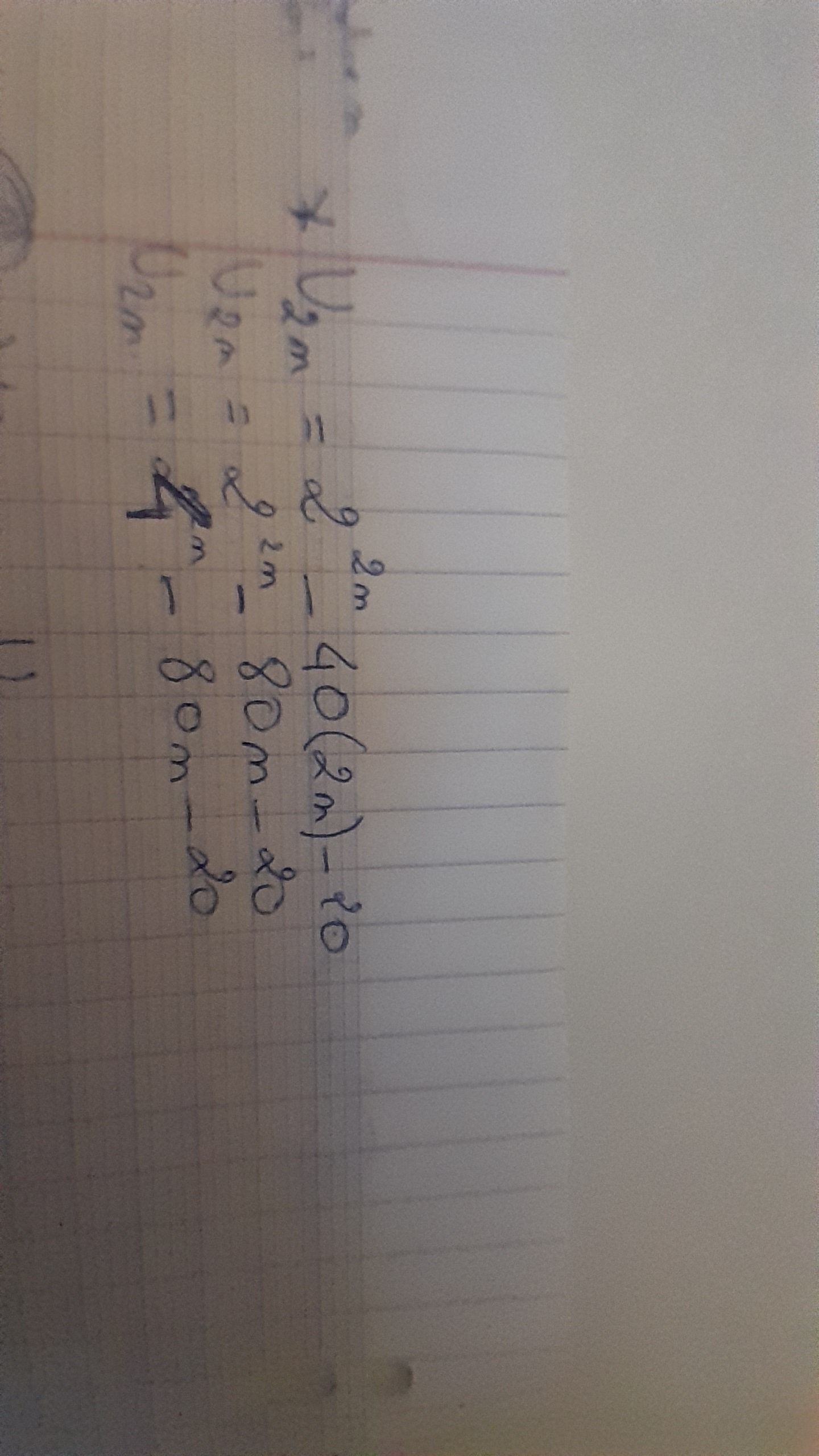
-
C'est correct.
-
Mm12 dernière édition par
@Noemi a dit dans Exercice suite numériques :
C'est correct.
Merci
2 ème question : demontrer que la suite Un=2n-40n-20 est croissante à partir du rang 6Alors j ai fait
Un+1-un
(2n+1-40(n+1)-20) - (2n-40-20)
2n+1-40-40-20-2n+40n+20
2n-40Pour n>6
2n>40
Pour n=5 2puissance5=32<40
Pour n=6 2 puissance 6= 64>40
La suite Un est donc croissante à partir du rang 6
-
La démarche est correcte mais l'absence de l'exposant rend difficile la compréhension.
Un+1−Un=(2n+1−40(n+1)−20)−(2n−40n−20)U_{n+1}-U_n=(2^{n+1}-40(n+1)-20)-(2^n-40n-20)Un+1−Un=(2n+1−40(n+1)−20)−(2n−40n−20)
Un+1−Un=2n+1−40n−40−20−2n+40n+20U_{n+1}-U_n=2^{n+1}-40n-40-20-2^n+40n+20Un+1−Un=2n+1−40n−40−20−2n+40n+20
Un+1−Un=2×2n−40−2nU_{n+1}-U_n=2\times 2^n-40-2^nUn+1−Un=2×2n−40−2n
Un+1−Un=2n−40U_{n+1}-U_n=2^n-40Un+1−Un=2n−40Pour n≥6n \geq 6n≥6
Pour n=6n= 6n=6 ; 2n=64>402^n= 64 \gt 402n=64>40
donc ....
-
Mm12 dernière édition par
@Noemi a dit dans Exercice suite numériques :
La démarche est correcte mais l'absence de l'exposant rend difficile la compréhension.
Un+1−Un=(2n+1−40(n+1)−20)−(2n−40n−20)U_{n+1}-U_n=(2^{n+1}-40(n+1)-20)-(2^n-40n-20)Un+1−Un=(2n+1−40(n+1)−20)−(2n−40n−20)
Un+1−Un=2n+1−40n−40−20−2n+40n+20U_{n+1}-U_n=2^{n+1}-40n-40-20-2^n+40n+20Un+1−Un=2n+1−40n−40−20−2n+40n+20
Un+1−Un=2×2n−40−2nU_{n+1}-U_n=2\times 2^n-40-2^nUn+1−Un=2×2n−40−2n
Un+1−Un=2n−40U_{n+1}-U_n=2^n-40Un+1−Un=2n−40Pour n≥6n \geq 6n≥6
Pour n=6n= 6n=6 ; 2n=64>402^n= 64 \gt 402n=64>40
donc ....La suite u n est croissante à partir du rang 6
-
C'est correct.
-
Mm12 dernière édition par
@Noemi a dit dans Exercice suite numériques :
C'est correct.
Ensuite faut déduire que tous les termes de cette suite sont strictement positig à partir du rang 9
U6= 2 puissance6-40(6)-20 = -196<0
U7 = 2 puiss 7-40(7)-20 = -172<0
U8 = -84<0
U9 = 132>0
-
C'est correct.
-
Mm12 dernière édition par
@Noemi a dit dans Exercice suite numériques :
C'est correct.
- on note vn = 2n-20 n carre
Demontrer que pour tout entier naturel n vn+1--vn=un
J ai fait (2n+1-20(n+1)carre)-2n+1-20(n carre+2n+1)-2n+20n carre =un
2n-40n-20=un
Déduisez sens variation et à partir de quel rang à ton vn>= 0
Un>0 pour n>= 9 donc vn+1-vn >0
Donc a suite est strictement croissante à partir du rang 9
-
Mm12 dernière édition par
@m12 a dit dans Exercice suite numériques :
@Noemi a dit dans Exercice suite numériques :
C'est correct.
- on note vn = 2n-20 n carre
Demontrer que pour tout entier naturel n vn+1--vn=un
J ai fait (2n+1-20(n+1)carre)-2n+1-20(n carre+2n+1)-2n+20n carre =un
2n-40n-20=un
Déduisez sens variation et à partir de quel rang à ton vn>= 0
Un>0 pour n>= 9 donc vn+1-vn >0
Donc a suite est strictement croissante à partir du rang 9@Noemi a dit dans Exercice suite numériques :
C'est correct.
Puis après il demande à partit de quel rang a t on vn>= 0
J ai fais v0= 2 puiss 0 - 20 (0) carre = 1 >0
J zi fais jusqu'à v11 = 2 puissance 11-20 (11) carre= 2048-2420= -372 <0Puis v12 = 4096-2880=1276 >0 donc positif
-
Les calculs sont justes.
-
Mm12 dernière édition par