Exprimer le volume d'une boite en fonction de x et résoudre

Bonsoir à tous,
j'ai un dm en math à faire, j'aimerais savoir si je n'ai pas commis d'erreur et il y a une question que je ne comprend pas alors si quelqu'un pouvait m'aider....

voilà le sujet :

1 détermination de la fonction :

On dispose d'une feuille cartonnée de 12 dm sur 10 dm. On souhaite contruire une boite parallélépipédique en repliant le long des 4 bords de la feuille une bande de largeur x. (voir shema)
En collant les bandes repliées, on obtient une boite ouverte dont on cherche le volume.

a) déterminer l'intervalle possible de la variable x

ma réponse : supérieur à 0, et inférieur à 5

b) Exprimer la longueur L, la largeur l et la hauteur h de cette boite en fonction de x

mes réponses : L = 12-2x ; l = 10-2x ; h = x

c) En déduire le volume V de la boite en fonction de x (vous donnerez la forme factorisée et la forme développée de la fonction et préciserez son domaine de définition et son unité).

mes réponses :
forme factorisée : V = (12-2x)(10-2x)x

forme développée : = x(120-24x-20x+4x²)
= x(120-44x-4x²)
= 120x-44x²+4x³

son domaine de définition : ]0,5[
son unité : dm3

2 représentation graphique
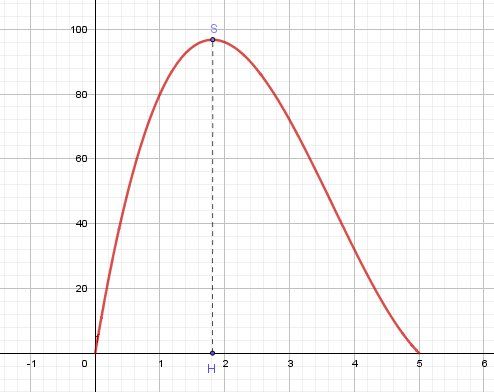
a Tableau de valeurs (à compléter)

x 0 - 0,5 - 1 - 1,5 - 2 - 2,5 - 3 - 3,5 - 4 - 4,5 - 5
V(x) 0 - 49,5 - 80 - 94,5 - 96 - 87,5 - 72 - 52,5 - 32 - 13,5 - 0

quel semble être le sens de variation de la fonction d'après ce tableau de valeur ?

ma réponse : croissant sur [0;2] et décroissant sur [2;5] (je ne suis pas sure de ma réponse, c'est aussi ma réponse à la dernière question tableau de variation...)

et voici la question que je ne comprends pas, je ne sais pas du tout ce que je dois faire....

b Recherche d'un point particulier. Dans l'intervalle qui vous semble le plus intéressant, calculer les images de 4 valeurs intermédiaires pour la variable x.

Ensuite je dois représenter la courbe et
a) determiner le volume maximal, pour quelle valeur de x est il obtenu ?
ma réponse : 96 dm3

b) pour quelle(s) valeur(s) le volume est-il égal à 60 dm3 ?
ma réponse ; x à peu près égal à 0.65 et à peu près égal à 3,3

c) pour quelle(s) valeur(s) le volume est-il strictement inférieur à 45 dm3 ?
ma réponse : [0 ; 0,5] et [3,7; 5]

d) pour quelle(s) valeur(s) le volume est-il strictement supérieur à 85 dm3?
ma réponse : [1,2 ; 2,6]

4 dresser le tableau de variation de la fonction. (fait mais je ne sais pas comment le reproduire ici....)

Merci à ceux qui pourront m'aider pour la question 2b et me dire si mes autres réponses sont correctes et bien "rédigées" (mon prof est très très pointilleux).

Bonsoir,

Je ne pourrai pas t'aider pour la rédaction ...

Compte tenu de la précision graphique, tout ce que tu as fait a l'air bon.

Pour la question que tu ne comprends pas : il s'agit simplement de choisir 4 valeurs de x proches de celle pour laquelle la fonction atteint son maximum et de déterminer ce maximum avec davantage de précision que tu ne l'as fait.

Tu devrais trouver un maximum atteint pour une valeur de x proche de 1,8. Il faudra modifier tes tableaux de variations en conséquence.

Sinon c'est bien.

Merci beaucoup d'avoir pris du temps pour regarder ce que j'avais fait. Donc les 4 valeurs que je devrais prendre sont 1,6 ; 1,7 ; 1.8 ; 1,9.
Je vous souhaite une bonne soirée

@paulene quels sont les calculs à faire pour trouver quel es la valeur de x pour que le volume de la boîte es au max SVP

@aroon Bonjour, (marque de politesse à ne pas oublier !!)

As-tu étudié les variations de la fonctions ?

Bonjour,

@aroon , tu n'as pas répondu à la question de @Noemi relative au sens de variation de la fonction.....

Si tu veux savoir la valeur exacte de $x$ pour que le volume de la boîte soit au maximum, cette valeur est $11−133\boxed{\dfrac{11-\sqrt{13}}{3}}$
Comme l'a indiqué @Thierry dans sa réponse ( il y a 14 ans) cette valeur est voisine de $1.8$ et si tu prends une valeur approchée sur la calculette , tu dois obtenir 1.8106....

Trouver cette valeur n'est pas le but de cet exercice qui est un exercice de Seconde.

Si tu connais le programme de Première (?) , tu peux faire ainsi :

Sur $] 0, 5 [$ , $V(x)=4x^3-44x^2+120x$
La dérivée vaut $V'(x)=12x^2-88x+120$
Cette dérivée est un polynôme du second degré.
Tu étudies le signe de $V^{'} (x)$ , ce qui te permet de déduire le sens de variation de la fonction $V$
La valeur de $x$ de $] 0, 5 [$ qui rend $V (x)$ maximal est la solution, sur $] 0, 5 [$ , de l'équation $12x^2-88x+120=0$ , d'où , après calculs, $x=11−133x=\dfrac{11-\sqrt{13}}{3}$

Conclusion : si tu connais déjà le programme de Première, tu peux faire les calculs, sinon, attends de le connaître.

Représentation graphique de la fonction $V$ sur $] 0, 5 [$