Intégrale de la fonction "Partie entière"

Bonsoir chers tous!
Veuillez svp m'aidez car je comprend pas cet exercice.
On me demande de calculer Calculer l'intégrale allant de 0 à 3 de E(x)dx où E(x) est la partie entière de x.
Franchement je ne sais pas comment m'y prendre. Je ne sais pas quelle fonction intégré car j'ai jamais rencontré une fonction de ce genre appelée partie entière. Veuillez svp m'éclairez car j'y vois rien.

Bonjour Wil-Fried ,

A partir de la représentation graphique (fonction en escalier), tu peux calculer directement l'aire, donc l'intégrale.
Pour $x∈[0;1[x\in[0;1[$ ; $E (x) = 0$
Pour $\in[1;2[$ ; $E (x) = 1$
.....

Bonjour,

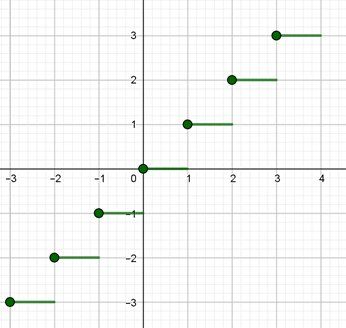
@Wil-Fried , pour t'éclairer , si besoin , sur la fonction partie entière E , je t'indique sa représentation graphique : PartieEntière.jpg
Par définition , pour tout naturel $n$ :
pour tout x de $[n, n + 1 [$ , $E (x) = n$

Dans ton exercice, tu ne t'intéresses qu'à la représentation graphique pour $x∈[0,3[x\in[0,3[$ .
Tu n'as qu'une somme d'aires de rectangles à calculer.

Tiens nous au courant si besoin.

@mtschoon Du coup mon résultat est bien 3 ??

@Wil-Fried
Oui
$0 + 1 + 2 = 3$

Bonjour,

Oui @Wil-Fried , tu as bien compris.
Le résultat est bien 3

Si tu veux un complement relatif aux intégrales des fonctions en escalier (dont fait partie la fonction partie entière), tu peux regarder ici.
https://www.youtube.com/watch?v=SINAal3qJAQ

@mtschoon Merciii.
J'ai un petit soucis svp, et c'est concernant l'écriture ici.
En fait j'ai des difficultés par exemple si je veux utiliser "intégrale" dans mon message je ne sais pas comment faire et bien d'autres symboles Mathématiques. Veuillez svp m'aider.

@Wil-Fried , si tu veux écrire correctement les formules mathématiques sur le forum, il faut que tu te mettes au Latex

Je te mets un lien ici :https://forum.mathforu.com/topic/163/comment-écrire-les-principales-expressions-mathématiques-work-in-progress

Par exemple, pour une intégrale , sans mettre d'espace entre et $ $, tu dois écrire :

$ \int_0^3 E(x)dx=3 $ et tu obtiens $∫03E(x)dx=3\int_0^3 E(x)dx=3$

@mtschoon Super! Merci

De rien @Wil-Fried .
Bien sûr , il faut une certaine habitude pour pouvoir écrire les principales expressions.