Recherche d'un domaine de définition
-
Jack Lundula dernière édition par Noemi

Salut tout le monde j'ai un devoir de math... on demande de trouver le domaine de définition
Y= V(2sin2x - V3)
-
Bonsoir Jack-Lundula,
La fonction est-elle ?
Y=2sin(2x)−3Y=\sqrt{2sin(2x)-\sqrt3}Y=2sin(2x)−3
-
Jack Lundula dernière édition par

@Noemi oui , je ne savais pas comment placer la Racine carrée
-
Tu dois résoudre l'inéquation :
sin(2x)≥32sin(2x) \geq \dfrac{\sqrt3}{2}sin(2x)≥23
-
mtschoon dernière édition par mtschoon

Bonjour,
@Jack-Lundula , un conseil pour simplifier ton travail : la fonction xxx-> sin(2x)sin(2x)sin(2x) est périodique.
Tu peux chercher sa période T (la plus petite, strictement positive) et travailler sur [0;T][0 ;T][0;T]
Tu généraliseras sur RRR pour la conclusion.
-
Jack Lundula dernière édition par

@mtschoon merci , le problème ce que je dois travailler sur [0,2pi] mais je ne sais pas comment faire... pourrais tu m'aider ?
-
Jack Lundula dernière édition par

@Noemi merci beaucoup ,je pense que là on aura une double inéquation
-
mtschoon dernière édition par mtschoon

@Jack-Lundula , tu n'avais pas indiqué sur quel intervalle tu devais travailler...
Prends l'habitude de donner les énoncés entiers.Bien sûr, la fonction xxx-> sin(2x) a pour période π\piπ
Tu peux travailler sur [0,π][0,\pi][0,π] et compléter par périodicité pour obtenir les résultats sur [π,2π][\pi,2\pi][π,2π]
Mais puisque l'énoncé te parle de [0,2π][0,2\pi][0,2π], tu peux travailler directement sur [0,2π][0,2\pi][0,2π], si tu le souhaites.Je te suggère de commencer à résoudre sin(2x)=32sin(2x)=\dfrac{\sqrt 3}{2}sin(2x)=23
Regarde la méthode de ton cours.
32=sinπ3\dfrac{\sqrt 3}{2}=sin\dfrac{\pi}{3}23=sin3π (angle remarquable)
Tu peux te servir du cercle trigonométrique ou bien tu résous l'équation sin(2x)=sinπ3sin(2x)=sin\dfrac{\pi}{3}sin(2x)=sin3π qui est de la forme sina=sinbsina=sinbsina=sinbRappel sur RRR :
sina=sinbsina=sinbsina=sinb <=> a=b [2π]a=b\ [2\pi]a=b [2π] ou a=π−b [2π]a=\pi-b\ [2\pi]a=π−b [2π]
Il faudra restreindre les valeurs de x à l'intervalle sur lequel tu travailles.
Sur [0,2π][0,2\pi][0,2π], tu dois trouver 4 valeurs
Si tu travailles sur [0,π][0,\pi][0,π], tu en trouveras 2Tiens nous au courant de ton avancé.
-
Jack Lundula dernière édition par

@mtschoon merci beaucoup pour votre aide j'ai pu résoudre l'exercice. merci encore pour votre patience
-
Peux-tu indiquer les intervalles solutions que tu as trouvés ?
-
mtschoon dernière édition par

Bonjour,
De rien @Jack-Lundula , mais on ne sait guère si tu as trouvé les bonnes réponses...
Je t'indique, sur le tableau joint, les 4 valeurs de [0,2π][0,2\pi][0,2π]qui annulent sin(2x)−32sin(2x)-\dfrac{\sqrt 3}{2}sin(2x)−23 c'est à dire les 4 valeurs telles que sin(2x)=32sin(2x)=\dfrac{\sqrt 3}{2}sin(2x)=23
Bien sûr, dans chaque case que j'ai laissé vide, il faut mettre les signes (+ ou -), pour en déduire l'ensemble de définition de la fonction f
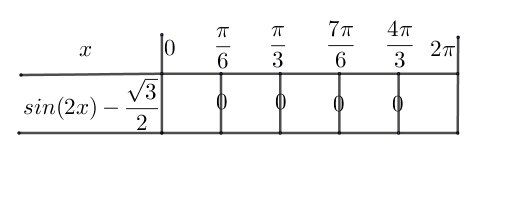
Si tu le souhaites, tu peux indiquer si tu as bien trouvé ces 4 valeurs et les signes mis dans les cases vides. Nous vérifierons.
Bon travail.
-
mtschoon dernière édition par

Bonjour,
Pour vérification éventuelle :
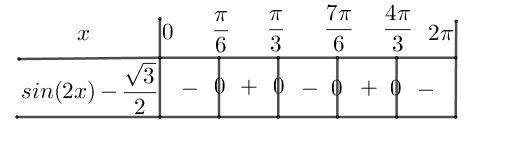
Domaine D de définition de f sur [0,2π][0,2\pi][0,2π] :
D=[π6,π3]∪[7π6,4π3]D=\biggr[\dfrac{\pi}{6},\dfrac{\pi}{3}\biggr]\cup\biggr[\dfrac{7\pi}{6},\dfrac{4\pi}{3}\biggr]D=[6π,3π]∪[67π,34π]
-
Jack Lundula dernière édition par

@mtschoon Merci infiniment pour votre aide , j'avais déjà rendu mon devoir par mail, et oui , j'ai trouvé ces réponses.
Merci encore, là maintenant je suis rassuré.
-
Jack Lundula dernière édition par

@Jack-Lundula Svp quelle est le logiciel ou l'application qui me permettrait de rédiger plus facilement les symboles mathématiques ?
-
mtschoon dernière édition par mtschoon

@Jack-Lundula , bonsoir,
C'est très bien d'être arrivé au bout de ton exercice.
Pour les formules mathématiques, ici on utilise le Latex.
Si tu veux t'entraîner, regarde ici :
https://forum.mathforu.com/topic/163/comment-écrire-les-principales-expressions-mathématiques-work-in-progress
-
Jack Lundula dernière édition par

@mtschoon merci beaucoup
-
mtschoon dernière édition par

@Jack-Lundula de rien et bon travail !