dérivation et polynome de degré 3
-
Livindiam Livin dernière édition par

Bonjour
Je dois déterminer l'expression d'une fonction f avec les données suivants :
- A(0;1) et B(1;1) sont des points par lesquels la courbe C passe
- équation de la tangente passant par A : y=-1,25x + 1
- équation de la tangente passant par B : y= 1,75x - 1,75
- f est une fonction polynome de degré 3
j'ai essayé de déterminer a avec les coordonnées des points mais le résultat emmène à 0, ce qui est impossible si on veut un polynome de degré 3
Merci pour toute aide afin que je puisse poursuivre cet exercice
-
@Livindiam-Livin Bonjour,
Indique tes calculs.
Soit f(x)=ax3+bx2+cx+df(x) = ax^3+bx^2+cx+df(x)=ax3+bx2+cx+d
Ecris un système à partir de :
f(0)=1f(0)= 1f(0)=1
f(1)=1f(1)=1f(1)=1
f′(0)=−1,25f'(0)=-1,25f′(0)=−1,25
f′(1)=1,75f'(1)=1,75f′(1)=1,75
-
Livindiam Livin dernière édition par

@Noemi Comment ? Je n'ai pas vu de leçon sur comment écrire un système à partir de nombre
-
@Livindiam-Livin
Soit f(x)=ax3+bx2+cx+df(x) = ax^3+bx^2+cx+df(x)=ax3+bx2+cx+d
A partir des données de l'énoncé :
f(0)=1f(0)= 1f(0)=1 donne : a×03+b×02+c×0+d=1a\times0^3+b\times 0^2+c\times0+d= 1a×03+b×02+c×0+d=1, d'ou d=1d= 1d=1f(1)=1f(1)=1f(1)=1 donne : ...
Calcul de la dérivée :
f′(x)=3ax2+.....f'(x)= 3ax^2+ .....f′(x)=3ax2+.....
puis
f′(0)=−1,25f'(0)=-1,25f′(0)=−1,25 donne : ....f′(1)=1,75f'(1)=1,75f′(1)=1,75 donne : ....
Je te laisse poursuivre les calculs.
-
mtschoon dernière édition par

Bonsoir,
@Livindiam-Livin , une remarque au sujet d'une équation de tangente que tu indiques.
Cela n'a pas de répercussion sur les calculs vu que c'est le coefficient directeur qui compte , mais il ya une erreur tout de même.Tangente en B(1,1) :
y=f′(1)(x−1)+f(1)y=f'(1)(x-1)+f(1)y=f′(1)(x−1)+f(1)<=> y=1.75(x−1)+1y=1.75(x-1)+1y=1.75(x−1)+1 <=>y=1.75x−0.75\boxed{y=1.75x-0.75}y=1.75x−0.75Si tu veux vérifier tes calculs, je t'indique quelques résultats.
f(x)=ax3+bx2+cx+df(x)=ax^3+bx^2+cx+df(x)=ax3+bx2+cx+d
f′(x)=3ax2+2bx+cf'(x)=3ax^2+2bx+cf′(x)=3ax2+2bx+cf(0)=f(0)=f(0)= <=> d=1d=1d=1
f(1)=1f(1)=1f(1)=1 <=> a+b+c+d=1a+b+c+d=1a+b+c+d=1
f′(0)=−1.25f'(0)=-1.25f′(0)=−1.25 <=> c=−1.25c=-1.25c=−1.25
f′(1)=1.75f'(1)=1.75f′(1)=1.75 <=> 3a+2b+c=1.753a+2b+c=1.753a+2b+c=1.75Tu connais donc déjà ccc et ddd
En remplaçant ccc et ddd par leurs valeurs dans les deux autres équations, tu obtiens :
{a+b=1.253a+2b=3\begin{cases}a+b=1.25\cr 3a+2b=3\end{cases}{a+b=1.253a+2b=3Après résolution, tu dois trouver : a=0.5a=0.5a=0.5 et b=0.75b=0.75b=0.75
donc f(x)=0.5x3+0.75x2−1.25x+1f(x)=0.5x^3+0.75x^2-1.25x+1f(x)=0.5x3+0.75x2−1.25x+1
Bons calculs !
-
mtschoon dernière édition par

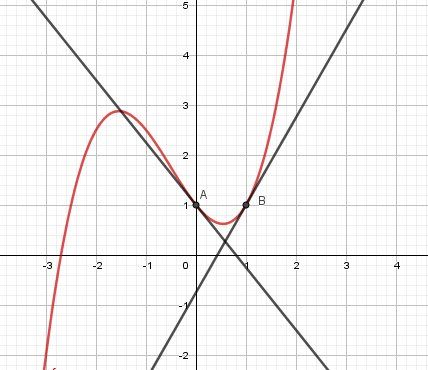
Illustration graphique, avec les résultats obtenus ( et la modification proposée pour la tangente en B)
-
Livindiam Livin dernière édition par

@mtschoon C'est plus clair à présent ! Je refais cela sans les réponses pour m'assurer que c'est compris, merci !
-
mtschoon dernière édition par

@Livindiam-Livin ,
De rien. Bons calculs .
-
Livindiam Livin dernière édition par

@mtschoon Rebonjour
J'ai refait l'exercice en multiplier par 2 : a +b soit 2a+2b= 2,5
j'ai laisser 3a+2b=3ensuite j'ai isoler 2b dans 3a+2b pour trouver que 2b=a
mais ensuite lorsque je remplace dans 2a+2b je ne trouve pas le bon résulat
Ai- je manquer une étape ?
-
mtschoon dernière édition par

Tu as un peu compliqué car en retranchant membre à membre les deux égalités, tu obtiens directement a=0.5a=0.5a=0.5
Si tu préfères, je regarde ce que tu as fait
3a+2b=33a+2b=33a+2b=3 donc 2b=3−3a2b=3-3a2b=3−3a
En remplaçant dans la seconde équation, tu obtiens
2a+3−3a=2.52a+3-3a=2.52a+3−3a=2.5 donc −a=2.5−3-a=2.5-3−a=2.5−3 donc −a=−0.5-a=-0.5−a=−0.5 donc a=0.5a=0.5a=0.5
-
Livindiam Livin dernière édition par

@mtschoon Merci !
-
mtschoon dernière édition par

De rien @Livindiam-Livin et bon travail !