résoudre équation avec cos et sin
-
Livindiam Livin dernière édition par

Bonjour !
Je suis en train de résoudre un exercice, j'aimerais savoir si je ne suis pas sur la mauvaise voie.
Tout d'abord voici le début de l'énoncé :
On considère l'équation (E) : 2sin^2 (x) + sin (x) -1 = 0
On doit résoudre cette équation dans l'intervalle [0,2pi[
On pose X = sin (x)
Question 1 changé l'équation avec X = sin (x)
: J'ai donc changé l'équation (comme demandé) en 2X^2 + X -1 = 0Question 2 : Résoudre l'équation
Ensuite j'ai résolu en faisant delta et en trouvant x1=-1 et x2=1/2Ensuite on nous demande en question 3 de déterminer les solutions dans l'intervalle donné ci dessus.
Dans un premier temps, les réponses sont-elles justes ?
Ensuite, faut-il pour cette intervalle donner en solutions des résultats avec 2Kpi ?
Les questions suivantes de l'exercice sont similaires mais avec cos (je les mettrais si besoin plus tard)Merci pour toutes aides !
-
@Livindiam-Livin Bonjour,
Les réponses sont correctes.
Il reste à résoudre :
sin(x)=−1sin(x)= -1sin(x)=−1 et sin(x)=12sin(x)= \dfrac{1}{2}sin(x)=21
Tu calcules les solutions générales puis celles sur l'intervalle indiqué.
-
Livindiam Livin dernière édition par

@Noemi sin(x) = -1 pour x= -pi/2 et sin(x)= 1/2 pour x = pi/6 et dans l'intervalle je fais -pi/2 + 2kpi et pi/6 + 2kpi ?
-
Attention, pour sin(x)=12sin(x)=\dfrac{1}{2}sin(x)=21 tu as deux solutions, il manque : x=5π6+2kπx= \dfrac{5\pi}{6}+2k\pix=65π+2kπ
Pour déterminer les solutions sur l'intervalle [0;2π][0;2\pi][0;2π],tu fais varier kkk.
-
Livindiam Livin dernière édition par

@Noemi ainsi je rajoute 2kpi après les trois solutions ? Merci
-
Ecrire x=−π2+2kπx=-\dfrac{\pi}{2}+2k\pix=−2π+2kπ correspond à l'ensemble des solutions de l'équation.
Il faut déterminer celles qui appartiennent à l'intervalle [0;2π][0;2\pi][0;2π]
si k=0k=0k=0 ; x=−π2x=-\dfrac{\pi}{2}x=−2π valeur qui n'appartient pas à l'intervalle.
si k=1k= 1k=1 ; x=....x= ....x=....Je te laisse poursuivre.
-
Livindiam Livin dernière édition par

@Noemi Je n'ai pas très bien compris...Je vais essayer de faire un cercle trigonométrique
-
Oui, place chaque solutions sur le cercle trigonométrique et déduis-en les valeurs correspondantes de xxx.
-
Livindiam Livin dernière édition par

@Noemi je ne parvient pas à visualiser sur mon cercle l'intervalle 0, 2pi
Est ce toute la partie droite ?
-
Livindiam Livin dernière édition par

@Livindiam-Livin Ensuite, on nous demande de déterminer avec un raisonnement analogue les solutions de l'équation (F) = cos^2 (x) + 2sin^2 (x) = 2 dans l'intervalle [-pi,pi]
J'ai repris le même cheminement que pour la première partie en posant cette foi-ci Y = cos (x)
soit Y^2 + 2X^2 -2 = 0
Ensuite, j'ai essayé de résoudre cette équation de deux façons :1e façon : je me suis aidée de la partie précédente avec 2X^2 + X -1 = 0
2X^2 = -X +1A partir de là j'ai changé 2X^2 par -X+1 ce qui me donne
Y^2 - X - 1 = 0
j'ai fait delta mais les résultats que je trouve me semblent étranges à savoir
x1 = 1 - racine de 5 / 2 et x2 = 1 + racine de 5 / 2J'ai essayé d'une autre façon avec cos ^2( x) + sin^2 (x) =1
- sin ^2(x) + 1 = cos ^2 (x)
- sin ^2 (x) +1 - sin (x) -1 = 0 en utilisant la formule du cours du théorème de pythagore
- sin ^2 (x) - sin (x) = 0Puis j'ai fait delta et trouvé x1 = 0 et x2 = -1
Merci pour tout feed-back/conseils/aides : j'ai essayé d'être le plus claire possible dans mon raisonnement, n'hésiter pas à faire des remarques si quelque chose est flou
-
@Livindiam-Livin Bonjour
Pour le cercle trigonométrique, regarde ce cours : https://www.mathforu.com/seconde/cercle-trigonometrique/
Pour l'autre question.
En utilisant la relation cos2(x)+sin2(x)=1cos^2(x)+sin^2(x)= 1cos2(x)+sin2(x)=1 l'expression devient :
sin2(x)+1=2sin^2(x)+1=2sin2(x)+1=2, soit sin2(x)=1sin^2(x)= 1sin2(x)=1
Equation à résoudre
-
mtschoon dernière édition par mtschoon

Bonjour,
@Livindiam-Livin , si ça peut t'éclairer je te fais une représentation graphique des solutions sur le cercle trigonométrique.
Pour la première équation, les solutions, sur RRR, sont :
a) x=π6+2kπx=\dfrac{\pi}{6}+2k\pix=6π+2kπ et x=5π6+2kπx=\dfrac{5\pi}{6}+2k\pix=65π+2kπ , k∈Zk\in Zk∈Z
Pour avoir les solutions sur I=[0,2π[I=[0,2\pi[I=[0,2π[, on prend k=0k=0k=0 ce qui donne x=π6x=\dfrac{\pi}{6}x=6π et x=5π6x=\dfrac{5\pi}{6}x=65π
b) x=−π2+2kπx=-\dfrac{\pi}{2}+2k\pix=−2π+2kπ, k∈Zk\in Zk∈Z
Pour avoir la solution sur I=[0,2π[I=[0,2\pi[I=[0,2π[, on prend k=1k=1k=1 ce qui donne x=3π2x=\dfrac{3\pi}{2}x=23πPour illustrer l'intervalle I=[0,2π[I=[0,2\pi[I=[0,2π[ :
(OA→,OM→)(\overrightarrow{OA},\overrightarrow{OM})(OA,OM) a une mesure xxx comprise entre 000 et 2π2\pi2π
MMM part de AAA pour x=0x=0x=0, MMM se déplace dans le sens trigonométrique (voir "flèche avec +"), MMMest en BBB pour x=π2x=\dfrac{\pi}{2}x=2π, MMMest en CCC pour x=πx=\pix=π, MMMest en DDD pour x=3π2x=\dfrac{3\pi}{2}x=23π et arrive ne AAA pour x=2πx=2\pix=2π (non pris dans l'intervalle , car crochet ouvert).Sur cet intervalle I, les solutions sont :
lorsque MMM est en E (x=π6)E\ \boxed{(x=\dfrac{\pi}{6})}E (x=6π) ,
lorsque MMM est en FFF (x=π−π6=5π6)\boxed{(x=\pi-\dfrac{\pi}{6}=\dfrac{5\pi}{6})}(x=π−6π=65π) et
lorsque MMM est en DDD (x=3π2)\boxed{(x=\dfrac{3\pi}{2})}(x=23π)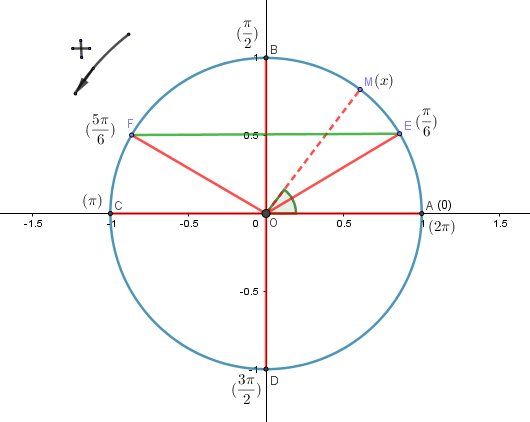
-
mtschoon dernière édition par mtschoon

Pour la seconde équation,
sin2(x)=1sin^2(x)=1sin2(x)=1 <=> sin(x)=1sin(x)=1sin(x)=1 ou sin(x)=−1sin(x)=-1sin(x)=−1
Sur RRR, les solutions sont x=π2+2kπx=\dfrac{\pi}{2}+2k\pix=2π+2kπ , k∈Zk\in Zk∈Z et x=−π2+2kπx=\dfrac{-\pi}{2}+2k\pix=2−π+2kπ , k∈Zk\in Zk∈ZCette fois, il faut obtenir les solutions sur J=[−π,π[J=[-\pi,\pi[J=[−π,π[ ; il faut donc prendre k=0k=0k=0 et l'on obtient x=−π2x=-\dfrac{\pi}{2}x=−2π et x=π2x=\dfrac{\pi}{2}x=2π
Pour illustrer l'intervalle J=[−π,π[J=[-\pi,\pi[J=[−π,π[ :
(OA→,OM→)(\overrightarrow{OA},\overrightarrow{OM})(OA,OM) a une mesure xxx comprise entre −π-\pi−π et π\piπMMM part de CCC pour x=−πx=-\pix=−π
MMM se déplace dans le sens trigonométrique .
MMM est en DDD pour x=−π2x=-\dfrac{\pi}{2}x=−2π , MMM est en AAA pour x=0x=0x=0 , MMM est en BBB pour x=π2x=\dfrac{\pi}{2}x=2π , et MMM arrive en CCC pour x=πx=\pix=π (non pris dans l'intervalle , car crochet ouvert).Sur cet intervalle J, les solutions sont :
lorsque M est en D (x=−π2)D\ \boxed{(x=-\dfrac{\pi}{2})}D (x=−2π) et lorsque M est en B (x=π2)B \ \boxed{(x=\dfrac{\pi}{2})}B (x=2π)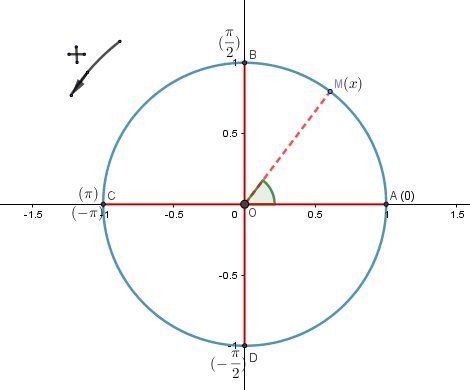
Bonnes réflexions éventuelles.
-
Livindiam Livin dernière édition par

@mtschoon Donc pour l'intervalle c'est un peu comme si c'était un tour complet sans prendre les solutions de 2pi ?
De plus au lieu d'écrire 3pi/2 peut on écrire -pi/2 ?
-
Livindiam Livin dernière édition par

@Livindiam-Livin Je ne comprends pas pourquoi on prend pour k=1 et pas pour k=0 comme pour les deux autres solutions
-
Livindiam Livin dernière édition par

@mtschoon Pour cette question j'ai bien compris merci !
-
mtschoon dernière édition par

@Livindiam-Livin , j'essaie de répondre à tes deux questions.
Première équation, par exemple :
Pour x∈Ix\in Ix∈I avec I=[0,2π]I= [0,2\pi]I=[0,2π], le point M(x)M(x)M(x) peut faire un tour entier de la position A(x=0A (x=0A(x=0) jusqu'à la position A(x=2π)A (x=2\pi)A(x=2π),en "tournant" dans le sens positif (trigonométrique).
Les solutions de l'équation doivent appartenir à cet intervalle IIIJe prends des valeurs approchées (ce qu'il ne faut pas faire dans un devoir) pour te faire comprendre.
2π≈6.282\pi\approx 6.282π≈6.28 d'où I≈[0,6.28[I\approx[0,6.28[I≈[0,6.28[
π6≈0.52\dfrac{\pi}{6} \approx 0.526π≈0.52
5π6≈2.62\dfrac{5\pi}{6} \approx 2.6265π≈2.62
3π2≈4.71\dfrac{3\pi}{2} \approx 4.7123π≈4.71
C'es 3 valeurs approchées 0.52, 2.62, 4.71 sont bien comprises entre 0 et 6.28 ; elle conviennent.
Si tu avais pris comme mesure, pour le point D la valeur −π2-\dfrac{\pi}{2}−2π, elle n'aurait pas convenue car −π2-\dfrac{\pi}{2}−2π est une valeur négative ( voisine de -1.57) qui n'est pas comprise entre 0 et 6.28.Lorsque tu as les solutions sur RRR, tu déduis les valeurs de k pour que les solutions appartiennent à l'intervalle demandé.
Reposte si besoin.
-
mtschoon dernière édition par

Je tapais ma dernière réponse pendant que tu indiquais :
@Livindiam-Livin a dit dans résoudre équation avec cos et sin :
@mtschoon Pour cette question j'ai bien compris merci !
Si c'est le cas, c'est parfait, sinon reposte.
-
Livindiam Livin dernière édition par

@mtschoon J'ai compris merci
-
mtschoon dernière édition par

Donc, c'est parfait !