distance point plan terminale

bonsoir,

Je veut calculer la distance entre un point Z(0;0;0) le point qui se trouve à l'origine du repère et un plan DKC dont l'équation de plan est 2x + 8y + 3z + 1 = 0.

On me donne les coordonées des points D, K et C.

J'ai cherché et la piste que j'ai trouvé une formule : 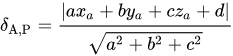mais elle ne me dit rien (pas vu en cours°

Est ce la bonne voie ?

Merci pour toute aide !

@Livindiam-Livin Bonsoir,

Tu peux utiliser cette formule.

@Noemi merci

@Livindiam-Livin

Pour avoir d'autres pistes, consulte ce lien : http://col89-larousse.ac-dijon.fr/IMG/pdf/Fiche_028_-_distance_d_un_point_a_un_plans.pdf

Bonjour,

@Livindiam-Livin , la formule donnée pour la distance d'un point à un plan $(P)$ est ce qu'il y a de plus rapide , bien sûr (c'est fait pour).

Soit $O (0, 0, 0)$ le point ( je l'appelle $O$ car la notation $Z$ ne me semble pas heureuse...)

Avec cette formule, la distance de $O$ au plan $(P$ ) est :
$d=∣2.0+8.0+3.0+1∣22+82+32=177d=\dfrac{|2.0+8.0+3.0+1|}{\sqrt{2^2+8^2+3^2}}=\dfrac{1}{\sqrt{77}}$

Si cette formule ne fait pas partie de ton cours, tu t'en passes mais c'est nettement plus long.

Piste (longue) , sans la formule usuelle.

En repère orthonormé ,
Soit $N→\overrightarrow{N}$ un vecteur normal au plan $(P)$ d'équation $2 x + 8 y + 3 z + 1 = 0$
$N→\overrightarrow{N}$ a pour coordonnées $(2, 8, 3)$

Soit $(D)$ la droite perpendiculaire à $(P)$ et passant par $O$
$(D)$ admet $N→\overrightarrow{N}$ comme vecteur directeur.

Représentation paramétrique de $(D)$ :
Soit $M (x, y, z)$
$OM→=kN→\overrightarrow{OM}=k\overrightarrow{N}$ , c'est à dire :
${x=2ky=8kz=3k\begin{cases}x=2k\cr y=8k\cr z=3k\end{cases}$

Soit $I$ le point d'intersection de $(D)$ avec $(P)$
Les coordonnées de $I$ sont solutions du système :
${x=2ky=8kz=3k2x+8y+3z+1=0\begin{cases}x=2k\cr y=8k\cr z=3k \cr 2x+8y+3z+1=0\end{cases}$

Par substitution des 3 premières équations dans la 4ème, après calculs, on obtient $k=−177k=-\dfrac{1}{77}$
$I$ a pour coordonnées $(−277,−877,−377)(-\dfrac{2}{77},-\dfrac{8}{77},-\dfrac{3}{77})$

La distance $d$ cherchée est $O I$

$d=OI=(−277−0)2+(−877−0)2+(−377−0)2d=OI=\sqrt{(-\dfrac{2}{77}-0)^2+(-\dfrac{8}{77}-0)^2+(-\dfrac{3}{77}-0)^2}$

$d=4+64+9772=77772=177d=\sqrt{\dfrac{4+64+9}{77^2}}=\sqrt{\dfrac{77}{77^2}}=\sqrt{\dfrac{1}{77}}$

$d=177\boxed{d=\dfrac{1}{\sqrt{77}}}$

CQFD.

@mtschoon Merci

De rien @Livindiam-Livin .
J'espère que maintenant c'est clair pour toi.

@Livindiam-Livin
Bonsoir, je me permet de répondre à ton message étant moi-même en term spé maths.
Il y a un gros flou autour de cette formule, les enseignants ne savent pas vraiment si elle fait partie du programme du bac, personnellement je l'ai rajouté à mon cours au cas où, elle est bien utile et bien + rapide à utiliser.

Bonjour,

C'est vrai @lysecht qu'il y a un flou...

La formule directe de la distance d'un point à un plan n'est pas "exigible au programme"...

Cela n'est pas très clair !

Alors, il vaut mieux la connaître mais pouvoir s'en passer.

@lysecht Bonsoir,

Je n'ai jamais rencontré cette formule... En effet c'est toujours un plus dans le cours, et elle n'est pas si compliqué à comprendre.