Probabilité de A sachant B

Bonjour à tous, un ami m'a posé cette question et ce que je pensais au départ comme un "jeu d'enfant" sachant le peu d'inconnu du problème me paraît finalement assez difficile...
Voici la situation... Nous sommes sur un match de tennis opposant le joueur J1 au joueur J2.
Le match se joue au meilleur des 3 sets, donc J1 peut gagner 2 sets à 0 ou 2 sets à 1, et symétriquement pour J2.
Voici toute les probabilités connu :
P(W1) : victoire de J1
P(W2) : victoire de J2
P(W1_20) : victoire de J1 2 sets à 0
P(W1_21) : victoire de J1 2 sets à 1
P(W2_20) : victoire de J2 2 sets à 0
P(W2_21) : victoire de J2 2 sets à 1
P(A1) : J1 gagne le 1er set
P(A2) : J2 gagne le 1er set
Quelle est donc l'inconnu me diriez-vous ? Et bien je cherche à connaître la probabilité que le joueur 1 gagne le 1er set et gagne le match, je cherche donc à connaître P(W1|A1).
Quelqu'un aurait une idée de la façon de procéder ?
Merci d'avance pour votre aide,

@Rodgerio Bonjour,

Regarde cet exercice similaire : https://forum.mathforu.com/topic/31619/probabilité-conditionnelles

Bonjour,

Il faut quant même prendre garde que les différentes probabilités dite connues ... ne sont pas indépendantes.

Par exemple : P(A2) = 1 - P(A1)
... et plusieurs autres dépendances.

Merci pour vos retours!
Oui ce n'est pas si simple, sachant qu'ici la proba qu'un joueur gagne le 1er set n'est pas équivalente à la proba qu'un joueur gagne le second set.
Je pense donc que malgré mon impression de départ, il n'est pas possible de calculer cette proba.
Merci pour votre réactivité dans tous les cas !

Bonjour,

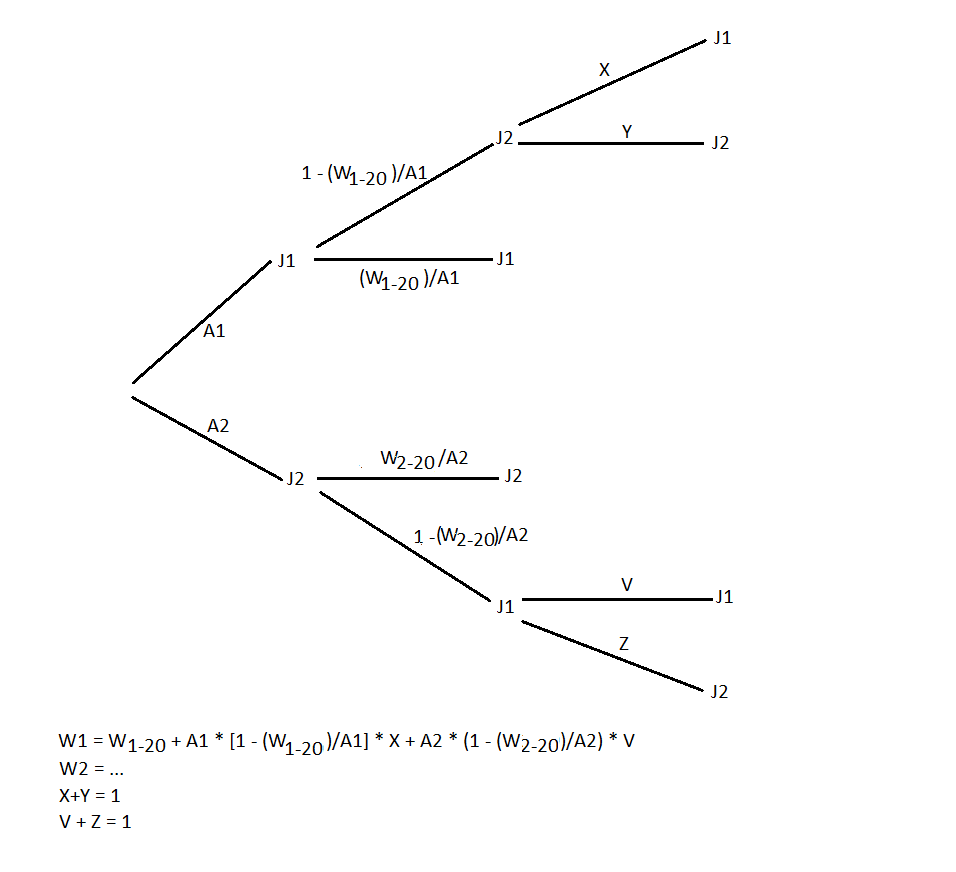
Et avec un arbre ?

On peut calculer X, Y ,Z et V à partir des 4 équations en bas du dessin.

La deuxième est à écrire ... et les autres à comprendre et vérifier.

Avec toujours la remarque que les probabilités dites connues ne sont pas indépendantes ...

Sans titre.png